题目内容
已知数列{xn}的前n项和为Sn,若点Pn(xn,Sn)(n=1,2,…)都在斜率为k的同一条直线上(常数k≠0,1)
(1)求证:{xn}是等比数列;
(2)设数列{xn}的公比为f(k),bn=-f(bn-1),b1=-1,Cn=bnbn+1,求C1+C2+…+Cn.
(1)求证:{xn}是等比数列;
(2)设数列{xn}的公比为f(k),bn=-f(bn-1),b1=-1,Cn=bnbn+1,求C1+C2+…+Cn.
分析:(1)由an+1=Sn+1-Sn着手考虑,把点Pn、Pn+1的坐标代入直线y=kx+b,然后两式相减得xn+1与xn的关系式,最后整理为等比数列的形式即可.
(2)根据数列{xn}的公比为f(k),则f(k)=
,然后求出bn的通项公式和cn的通项公式,最后利用裂项求和法求出所求.
(2)根据数列{xn}的公比为f(k),则f(k)=
| k |
| k-1 |
解答:解:(1)∵
=
=k,∴
=
∴{xn}成G.P;
(2)∵f(k)=
,∴bn=-
从而bnbn-1=bn-bn-1,即
-
=-1(n≥2)∴bn=-
,∴Cn=
=
-
,∴∑Ck=1-
=
| Sn+1-Sn |
| xn+1-xn |
| xn+1 |
| xn+1-xn |
| xn+1 |
| xn |
| k |
| k-1 |
(2)∵f(k)=
| k |
| k-1 |
| bn-1 |
| bn-1-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| n |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:an+1=Sn+1-Sn是实现数列{an},由其前n项和Sn向an转化的重要桥梁;要熟悉等差数列的解析式形式:an=An+B即一次函数型,等比数列的解析式形式为:an=Aqn指数型函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
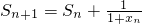 ,
,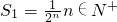
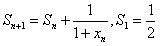 ,n∈N*。
,n∈N*。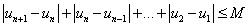 ,则称数列{un}为B-数列。问数列{xn}是B-数列吗? 并证明你的结论。
,则称数列{un}为B-数列。问数列{xn}是B-数列吗? 并证明你的结论。