Question

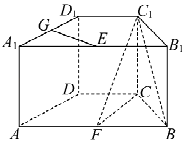
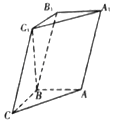
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．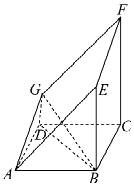

（1）求证：BD⊥平面ADG；
（2）求直线GB与平面AEFG所成角的正弦值．

Answer 1

【答案】（1）证明：在△BAD中，∵AB=2AD=2，∠BAD=60°．

由余弦定理BD2=AD2+AB2﹣2ABADcos60°， ，

∵AB2=AD2+DB2，

∴AD⊥DB，

在直平行六面体中，GD⊥平面ABCD，DB平面ABCD，∴GD⊥DB，

又AD∩GD=D，

∴BD⊥平面ADG．

（2）解：如图以D为原点建立空间直角坐标系D﹣xyz，

∵∠BAE=∠GAD=45°，AB=2AD=2，

∴A（1，0，0）， ， ，G（0，0，1）， ， ， ，

设平面AEFG的法向量 ， 令x=1，得 ，z=1，

∴ ，

设直线GB和平面AEFG的夹角为θ，

∴ ，

所以直线GB与平面AEFG所成角的正弦值为 ．

【解析】（1）求一条直线垂直于一个平面，证明这条直线与这个平面内相交的两条直线垂直即可；（2）先根据图形特点建立空间直角坐标系，求得平面AEFG的法向量，最终求得直线GB与平面AEFG所成角的正弦值.
【考点精析】通过灵活运用直线与平面垂直的判定和空间角的异面直线所成的角，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则即可以解答此题．