Question

（本小题共13分）

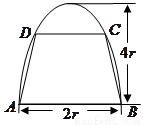如图，有一块半椭圆形钢板，其半轴长为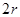，短半轴长为，计划将此钢板切割成等腰梯形的形状，下底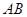是半椭圆的短轴，上底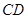的端点在椭圆上，记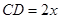，梯形面积为．

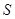（I）求面积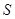以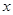为自变量的函数式，并写出其定义域；

（II）求面积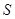的最大值．

 

 

 

 

Answer 1

【答案】

（I）

　，

其定义域为

（II）梯形面积的最大值为

【解析】解：（I）依题意，以的中点为原点建立直角坐标系（如图），则点的横坐标为．

点的纵坐标满足方程，

解得

　，

其定义域为．

（II）记，

则．

令，得．

因为当时，；当时，，所以是的最大值．

因此，当时，也取得最大值，最大值为．

即梯形面积的最大值为．