题目内容
如果sinx+cosx= ,且0<x<π,那么tanx的值是________.
,且0<x<π,那么tanx的值是________.
-
分析:先根据sinx+cosx的值和二者的平方关系联立求得cosx的值,进而根据同角三角函数的基本关系求得sinx的值,最后利用商数关系求得tanx的值.
解答:由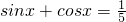 ,得
,得 
代入sin2x+cos2x=1得:(5cosx-4)(5cosx+3)=0
∴ 或
或 
当 时,得
时,得 
又∵0<x<π,
∴sinx>0,故这组解舍去
当 时,
时, ,
,
点评:本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的取值符号.

分析:先根据sinx+cosx的值和二者的平方关系联立求得cosx的值,进而根据同角三角函数的基本关系求得sinx的值,最后利用商数关系求得tanx的值.
解答:由
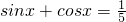 ,得
,得 
代入sin2x+cos2x=1得:(5cosx-4)(5cosx+3)=0
∴
 或
或 
当
 时,得
时,得 
又∵0<x<π,
∴sinx>0,故这组解舍去
当
 时,
时, ,
,
点评:本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的取值符号.

练习册系列答案
相关题目