题目内容
设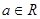 ,函数
,函数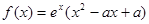 .
.
(Ⅰ)求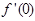 的值;
的值;
(Ⅱ)求函数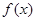 的单调区间.
的单调区间.
【答案】
(Ⅰ)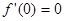 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)本小题首先需要对原函数求导得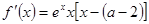 ,然后代入
,然后代入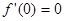 ;
;
(Ⅱ)本小题首先令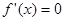 ,得
,得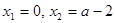 ,然后分析二根之间的关系,需要分类讨论,按
,然后分析二根之间的关系,需要分类讨论,按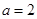 ;
;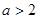 ;
;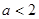 进行.
进行.
试题解析:(Ⅰ)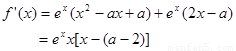
∴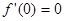 .
3分
.
3分
(Ⅱ)令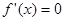 ,得
,得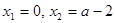 4分
4分
函数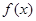 定义域为R,且对任意
定义域为R,且对任意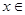 R,
R,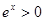 ,
,
当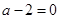 ,即
,即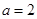 时,
时,
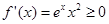 ,
,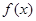 的单调递增区间是
的单调递增区间是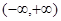 .
6分
.
6分
当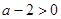 ,即
,即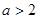 时,
时,
|
|
|
0 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
|
↘ |
|
↗ |
所以 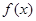 的单调递增区间是
的单调递增区间是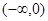 ,
,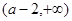 ,单调递减区间是
,单调递减区间是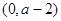 . 9分
. 9分
当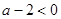 ,即
,即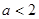 时,
时,
|
|
|
|
|
0 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
|
↘ |
|
↗ |
所以 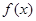 的单调递增区间是
的单调递增区间是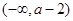 ,
,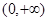 ,单调递减区间是
,单调递减区间是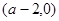 . 12分
. 12分
综上,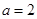 时,
时,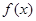 的单调递增区间是
的单调递增区间是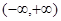 .
.
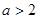 时,
时,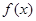 的单调递增区间是
的单调递增区间是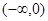 ,
,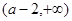 ,
,
单调递减区间是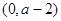 .
.
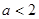 时,
时,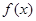 的单调递增区间是
的单调递增区间是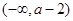 ,
,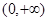 ,
,
单调递减区间是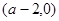 .
13分
.
13分
考点:1.导数分析原函数的单调性;2.分类讨论.

练习册系列答案
相关题目
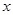
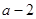
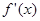
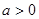 ,函数
,函数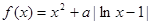
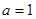 时,求曲线
时,求曲线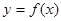 在
在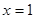 处的切线方程;
处的切线方程;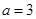 时,求函数
时,求函数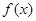 的单调区间;
的单调区间;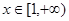 时,求函数
时,求函数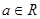 ,函数
,函数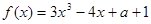 ,
, 的单调区间;
的单调区间;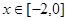 ,不等式
,不等式 恒成立,求
恒成立,求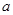 的取值范围。
的取值范围。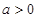 ,函数
,函数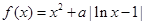 .
. 时,求函数
时,求函数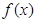 的单调增区间;
的单调增区间; 时,不等式
时,不等式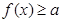 恒成立,实数
恒成立,实数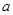 的取值范围.
的取值范围.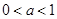 ,函数
,函数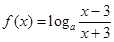 .
.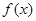 的定义域,并判断
的定义域,并判断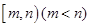 时,值域为
时,值域为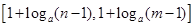 ,求
,求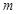 、
、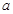 的取值范围.
的取值范围.