题目内容
已知向量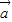 =(cos
=(cos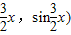 ,
,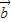 =(cos
=(cos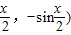 ,且x∈[-
,且x∈[-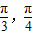 ].
].(1)求
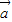 •
•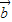 及|
及|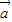 +
+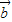 |;
|;(2)若f(x)=
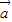 •
•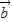 -|
-|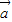 +
+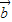 |,求f(x)的最大值和最小值.
|,求f(x)的最大值和最小值.
【答案】分析:(1)由向量数量积的坐标表示可得,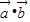 =cos
=cos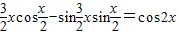 .
.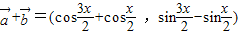 ,结合x∈[-
,结合x∈[-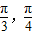 ],可求
],可求
(2)因为f(x)=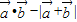 =cos2x-2cox=2cos2x-2cosx-1=2(cosx-
=cos2x-2cox=2cos2x-2cosx-1=2(cosx-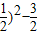 ,由x∈[-
,由x∈[-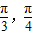 ],可得
],可得 ≤cosx≤1.结合二次函数的性质可求
≤cosx≤1.结合二次函数的性质可求
解答:解:(1)∵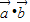 =cos
=cos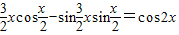 .
.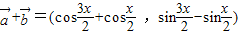
∴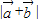 =
=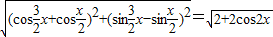 =2|cosx|
=2|cosx|
因为x∈[-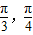 ],所以cosx>0.即
],所以cosx>0.即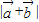 =2cosx.
=2cosx.
(2)因为f(x)=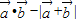 =cos2x-2cox=2cos2x-2cosx-1=2(cosx-
=cos2x-2cox=2cos2x-2cosx-1=2(cosx-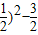 -
-
∵x∈[-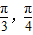 ],∴
],∴ ≤cosx≤1.
≤cosx≤1.
∴当cox= 时,f(x)取得最小值-
时,f(x)取得最小值-
当cosx=1,f(x)取得最大值-1.
点评:本题主要考查了向量的基本运算的坐标表示,向量的数量积的坐标表示,三角函数与向量的综合考查是高考的重点内容之一,要注意掌握
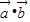 =cos
=cos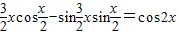 .
.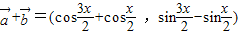 ,结合x∈[-
,结合x∈[-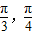 ],可求
],可求(2)因为f(x)=
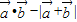 =cos2x-2cox=2cos2x-2cosx-1=2(cosx-
=cos2x-2cox=2cos2x-2cosx-1=2(cosx-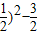 ,由x∈[-
,由x∈[-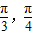 ],可得
],可得 ≤cosx≤1.结合二次函数的性质可求
≤cosx≤1.结合二次函数的性质可求解答:解:(1)∵
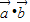 =cos
=cos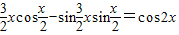 .
.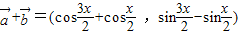
∴
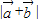 =
=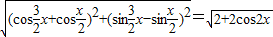 =2|cosx|
=2|cosx|因为x∈[-
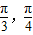 ],所以cosx>0.即
],所以cosx>0.即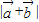 =2cosx.
=2cosx.(2)因为f(x)=
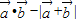 =cos2x-2cox=2cos2x-2cosx-1=2(cosx-
=cos2x-2cox=2cos2x-2cosx-1=2(cosx-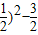 -
-
∵x∈[-
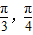 ],∴
],∴ ≤cosx≤1.
≤cosx≤1.∴当cox=
 时,f(x)取得最小值-
时,f(x)取得最小值-
当cosx=1,f(x)取得最大值-1.
点评:本题主要考查了向量的基本运算的坐标表示,向量的数量积的坐标表示,三角函数与向量的综合考查是高考的重点内容之一,要注意掌握

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |