题目内容
若两个向量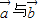 的夹角为θ,则称向量“
的夹角为θ,则称向量“ ”为“向量积”,其长度
”为“向量积”,其长度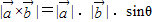 .
.若
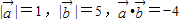 ,则
,则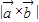 = .
= .
【答案】分析:由数量积的定义求出向量的夹角即可.
解答:解:因为若 ,
,
所以 ,
,
所以 ,
,
所以 =
= .
.
故答案为:3.
点评:本题主要考查新定义的理解和应用,利用定义求出sinθ的值是解决本题的关键.
解答:解:因为若
 ,
,所以
 ,
,所以
 ,
,所以
 =
= .
.故答案为:3.
点评:本题主要考查新定义的理解和应用,利用定义求出sinθ的值是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
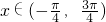 ,O为原点,若
,O为原点,若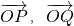 两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值.
两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值. ,O为原点,若
,O为原点,若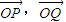 两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值.
两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值.