题目内容
平面内的点P(1,cosx),Q(cosx,1),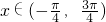 ,O为原点,若
,O为原点,若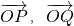 两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值.
两个向量的夹角为θ,求:f(x)=cosθ的最大值及相应的x的值.
解:由已知可得 f(x)=cosθ= =
= .∵
.∵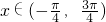 ,令t=cosx∈[-
,令t=cosx∈[- ,1],
,1],
可得 f(x)= =
= ≤1,当且仅当t=1时,等号成立.
≤1,当且仅当t=1时,等号成立.
故f(x)=cosθ的最大值为1,此时,t=cosx=1,x=0.
分析:由已知中点P(1,cosx),Q(cosx,1)的坐标,进而根据cosθ= ,我们可以求出余弦值f(x)的解析式,结合
,我们可以求出余弦值f(x)的解析式,结合 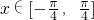 ,求得t=cosx的范围,由基本不等式
,求得t=cosx的范围,由基本不等式
求得到函数f(x)的最大值.
点评:本题主要考查的知识点是平面向量的数量积的坐标表示,平面向量数量积的运算,基本不等式的应用,注意角的范围,这是解题的易错点.
 =
= .∵
.∵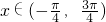 ,令t=cosx∈[-
,令t=cosx∈[- ,1],
,1],可得 f(x)=
 =
= ≤1,当且仅当t=1时,等号成立.
≤1,当且仅当t=1时,等号成立.故f(x)=cosθ的最大值为1,此时,t=cosx=1,x=0.
分析:由已知中点P(1,cosx),Q(cosx,1)的坐标,进而根据cosθ=
 ,我们可以求出余弦值f(x)的解析式,结合
,我们可以求出余弦值f(x)的解析式,结合 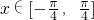 ,求得t=cosx的范围,由基本不等式
,求得t=cosx的范围,由基本不等式求得到函数f(x)的最大值.
点评:本题主要考查的知识点是平面向量的数量积的坐标表示,平面向量数量积的运算,基本不等式的应用,注意角的范围,这是解题的易错点.

练习册系列答案
相关题目
 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆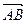 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转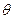 角,得到向量
角,得到向量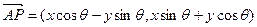 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转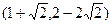 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标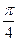 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线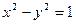 ,求原来曲线C的方程.
,求原来曲线C的方程. 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角,得到向量
角,得到向量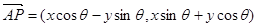 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线 ,求原来曲线C的方程.
,求原来曲线C的方程.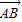 绕其起点沿逆时针方向旋转θ角,得到向量
绕其起点沿逆时针方向旋转θ角,得到向量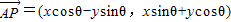 ,叫做把点B绕点A逆时针方向旋转θ角得到点P
,叫做把点B绕点A逆时针方向旋转θ角得到点P ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转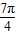 后得到点P,求点P的坐标
后得到点P,求点P的坐标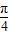 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.