Question

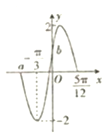
【题目】函数f（x）=Asin（2ωx+φ）（A＞0，ω＞0，|φ|＜）的部分图象如图所示

（1）求A，ω，φ的值；

（2）求图中a，b的值及函数f（x）的递增区间；

（3）若α∈[0，π]，且f（α）=，求α的值．

Answer 1

【答案】（1）；（2），递增区间为；（3）或.

【解析】

（1）利用函数图像可直接得出周期T和A，再利用，求出，

然后利用待定系数法直接得出的值。

（2）通过第一问求得的值可得到的函数解析式，令，再根据a的位置确定出a的值；令得到的函数值即为b的值；利用正弦函数单调增区间即可求出函数的单调增区间。

（3）令结合即可求得的取值。

解：（1）由图象知A=2，=-（-）=，

得T=π，

即=2，得ω=1，

又f（-）=2sin[2×（-）+φ]=-2，

得sin（-+φ）=-1，

即-+φ=-+2kπ，

即ω=+2kπ，k∈Z，

∵|φ|＜，

∴当k=0时，φ=，

即A=2，ω=1，φ=；

（2）a=--=--=-，

b=f（0）=2sin=2×=1，

∵f（x）=2sin（2x+），

∴由2kπ-≤2x+≤2kπ+，k∈Z，

得kπ-≤x≤kπ+，k∈Z，

即函数f（x）的递增区间为[kπ-，kπ+]，k∈Z；

（3）∵f（α）=2sin（2α+）=，

即sin（2α+）=，

∵α∈[0，π]，

∴2α+∈[，]，

∴2α+=或，

∴α=或α=．