Question

【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．

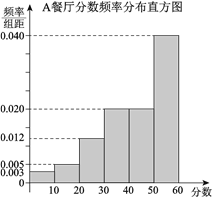
整理评分数据，将分数以为组距分成组： ， ， ， ， ， ，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：

B餐厅分数频数分布表
分数区间	频数

定义学生对餐厅评价的“满意度指数”如下：

分数
满意度指数

（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为的人数；

（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；

（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

Answer 1

【答案】（1）20（2） (3)见解析

【解析】试题分析：（Ⅰ）根据频率分布直方图求出频率为，可得人数；（Ⅱ）根据相互独立事件同时发生的概率及互斥事件发生的概率公式得结果；（Ⅲ）列出分布列，计算出学生对A，B两家餐厅评价的“满意度指数”的期望，比较即可.

试题解析：（Ⅰ）由对A餐厅评分的频率分布直方图，得

对A餐厅“满意度指数”为的频率为，

所以，对A餐厅评价“满意度指数”为的人数为．

（Ⅱ）设“对A餐厅评价‘满意度指数’比对B餐厅评价‘满意度指数’高”为事件C．

记“对A餐厅评价‘满意度指数’为”为事件；“对A餐厅评价‘满意度指数’为”为事件；“对B餐厅评价‘满意度指数’为”为事件；“对B餐厅评价‘满意度指数’为”为事件．

所以， ，

由用频率估计概率得： ， ．

因为事件与相互独立，其中， ．

所以

．

所以该学生对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高

的概率为．

（Ⅲ）如果从学生对A，B两家餐厅评价的“满意度指数”的期望角度看：

A餐厅“满意度指数”X的分布列为：

X
P

B餐厅“满意度指数”Y的分布列为：

Y
P

因为； ，

所以，会选择B餐厅用餐．