题目内容

设m，n是不同的直线，α，β是不同的平面，下列命题中正确的是（ ）
A．若m∥α，n⊥β，m⊥n，则α⊥β
B．若m∥α，n⊥β，m⊥n，则α∥β
C．若m∥α，n⊥β，m∥n，则α⊥β
D．若m∥α，n⊥β，m∥n，则α∥β
【答案】分析：利用线面平行、垂直的判定定理和性质定理及面面垂直的判定定理即可判断出答案．
解答：解：选择支C正确，下面给出证明．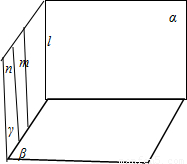
证明：如图所示：
∵m∥n，∴m、n确定一个平面γ，交平面α于直线l．
∵m∥α，∴m∥l，∴l∥n．
∵n⊥β，∴l⊥β，
∵l?α，∴α⊥β．
故C正确．
故选C．
点评：正确理解和掌握线面平行、垂直的判定定理和性质定理及面面垂直的判定定理是解题的关键．
练习册系列答案
相关题目
8、设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：①若α∥β，α∥γ，则β∥γ②若α⊥β，m∥α，则m⊥β③若m⊥α，m∥β，则α⊥β④若m∥n，?n?α，则m∥α其中真命题的序号是（　　）
4、设m，n是不同的直线，是不同的平面，则下列四个命题：①若α∥β，m?α，则m∥β，②若m∥α，n?α，则m∥n，③若α⊥β，m∥α，则m⊥β，④若m⊥α，m∥β，则α⊥β
其中正确的是（　　）
6、设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
（1）若n∥α，m∥β，α∥β，则n∥m；   （2）若m⊥α，n∥α，则m⊥n
（3）若α⊥γ，β⊥γ，则α∥β；         （4）若α∥β，β∥γ，m⊥α，则m⊥γ
其中真命题的个数是（　　）
设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
（1）
α∥β
α∥γ
?β∥γ；
（2）
α⊥β
m∥α
?m⊥β；
（3）
m⊥α
m∥β
?α⊥β；
（4）
m∥n
n?α
?m∥α．
其中，假命题是（　　）
A、（1）（2）
B、（2）（3）
C、（1）（3）
D、（2）（4）
设m、n是不同的直线，α、β是不同的平面，有以下四个命题：
①若m⊥α，n⊥α，则m∥n； 
②若α⊥β，m∥α，则m⊥β；
③若m上α，m⊥n，则n∥α；    
④若n⊥α，n⊥β，则β∥α．
其中，真命题的序号是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网