题目内容
已知二次函数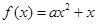
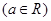
(1)当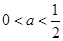 时,
时,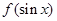
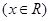 的最大值为
的最大值为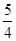 ,求
,求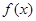 的最小值;
的最小值;
(2)对于任意的 ,总有
,总有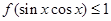 ,试求
,试求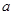 的取值范围.
的取值范围.
(1)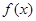 的最小值为
的最小值为 (2)
(2)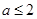
解析试题分析:(1)由已知条件可知,当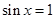 时
时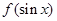 取得最大值,由此得到
取得最大值,由此得到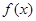 的解析式,进而得到f(x)的最小值.
的解析式,进而得到f(x)的最小值.
(2)根据已知条件结合换元法把命题转化为:任给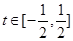 ,不等式
,不等式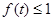 ,恒成立.由此入手,能够求出实数a的取值范围.
,恒成立.由此入手,能够求出实数a的取值范围.
试题解析:(1)由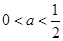 知
知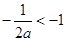 ,故当
,故当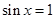 时
时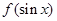 取得最大值
取得最大值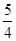 ,即
,即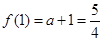 ,所以
,所以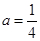 ,所以
,所以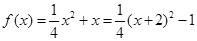 ,所以
,所以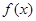 的最小值为
的最小值为 .
.
(2)对于任意的 ,总有
,总有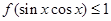 ,令
,令 ,
,
则命题转化为:任给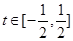 ,不等式
,不等式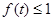 ,
,
当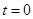 时,
时,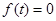 满足
满足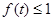 ;
;
当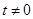 时,有
时,有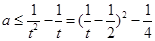 对于任意的
对于任意的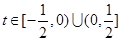 恒成立;
恒成立;
由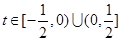 得
得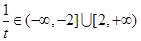 ,所以
,所以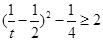 ,
,
所以要使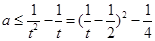 恒成立,则有
恒成立,则有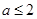 .
.
考点:二次函数的性质;正弦函数的定义域和值域.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
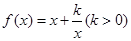 ,
,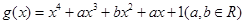 ,(1)若
,(1)若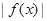 的最小值为2,求
的最小值为2,求 值;(2)设函数
值;(2)设函数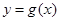 有零点,求
有零点,求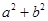 的最小值.
的最小值.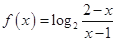 的定义域为集合
的定义域为集合 ,关于
,关于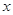 的不等式
的不等式 的解集为
的解集为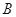 ,若
,若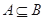 ,求实数
,求实数 的取值范围.
的取值范围.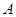 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的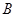 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足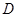 与
与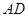 之间合建一个供水站
之间合建一个供水站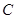 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3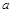 元和5
元和5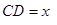 千米,设总的水管费用为
千米,设总的水管费用为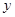 元,如图所示,
元,如图所示, 的函数表达式;
的函数表达式;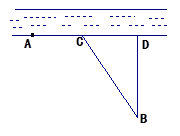
 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, .
.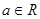 ,函数
,函数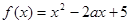 .
.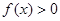 对任意
对任意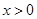 恒成立,求实数
恒成立,求实数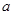 的最值范围;
的最值范围;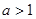 ,且函数
,且函数 的定义域和值域均为
的定义域和值域均为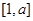 ,求实数
,求实数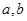 都是实数,且
都是实数,且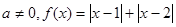 .
. 的解集;
的解集;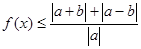 对满足条件的所有实数
对满足条件的所有实数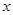 的取值范围.
的取值范围.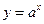 (
(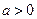 且
且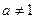 )与函数
)与函数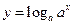 (
(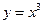 与
与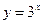 的值域相同;③函数
的值域相同;③函数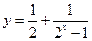 与
与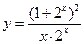 都是奇函数;④
都是奇函数;④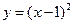 与
与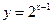 在区间
在区间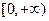 上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)