题目内容
设函数f(x)= ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,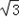 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=0且x∈(﹣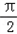 ,0),求tan2x;
,0),求tan2x;
(2)设△ABC的三边a,b,c依次成等比数列,试求f(B)的取值范围.
 ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,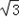 sin2x),x∈R.
sin2x),x∈R.(1)若f(x)=0且x∈(﹣
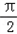 ,0),求tan2x;
,0),求tan2x;(2)设△ABC的三边a,b,c依次成等比数列,试求f(B)的取值范围.
解:(1)∵向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,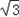 sin2x),
sin2x),
∴f(x)= =2cos2x+
=2cos2x+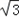 sin2x=cos2x+
sin2x=cos2x+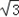 sin2x+1=2sin(2x+
sin2x+1=2sin(2x+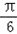 )+1
)+1
∵f(x)=0,
∴sin(2x+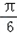 )=﹣
)=﹣
∵x∈(﹣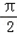 ,0),
,0),
∴2x+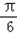 ∈
∈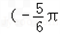 ,
,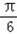 ),
),
∴2x+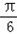 =﹣
=﹣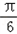
∴x=﹣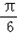 ,
,
∴tan2x=﹣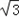 ;
;
(2)∵△ABC的三边a,b,c依次成等比数列,
∴b2=ac
由余弦定理可得: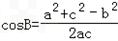 =
=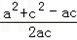 ≥
≥
∴0<B≤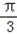 ,
,
∴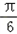 <2B+
<2B+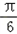 ≤
≤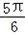
∴ ≤sin(2B+
≤sin(2B+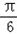 )≤1
)≤1
∴2≤f(B)≤3.
 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,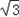 sin2x),
sin2x),∴f(x)=
 =2cos2x+
=2cos2x+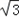 sin2x=cos2x+
sin2x=cos2x+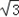 sin2x+1=2sin(2x+
sin2x+1=2sin(2x+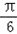 )+1
)+1∵f(x)=0,
∴sin(2x+
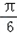 )=﹣
)=﹣
∵x∈(﹣
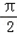 ,0),
,0),∴2x+
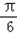 ∈
∈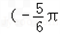 ,
,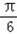 ),
),∴2x+
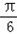 =﹣
=﹣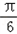
∴x=﹣
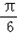 ,
,∴tan2x=﹣
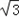 ;
;(2)∵△ABC的三边a,b,c依次成等比数列,
∴b2=ac
由余弦定理可得:
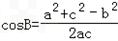 =
=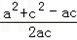 ≥
≥
∴0<B≤
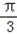 ,
,∴
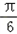 <2B+
<2B+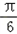 ≤
≤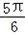
∴
 ≤sin(2B+
≤sin(2B+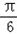 )≤1
)≤1∴2≤f(B)≤3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目