题目内容
若对实数x∈[10,+∞)恒有|logmx|≥2的实数m的取值范围________.
 ≤m<1或1<m
≤m<1或1<m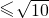
分析:由绝对值不等式的性质,将问题化为:logmx≤-2或logmx≥2对?x∈[10,+∞)恒成立.再对两个不等式进行讨论,分别得到符合题意的m的范围,最后综合可得实数m的取值范围.
解答:∵对?x∈[10,+∞),恒有|logmx|≥2成立,
∴不等式logmx≤-2或logmx≥2对?x∈[10,+∞)恒成立.
①若logmx≤-2,则m∈(0,1)
∴x≥m-2,可得10≥m-2,解之得
 ≤m<1;
≤m<1;②若logmx≥2,则m∈(1,+∞)
∴x≥m2,可得10≥m2,解之得1<m
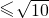
综上所述,可得实数m的取值范围是
 ≤m<1或1<m
≤m<1或1<m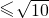
故答案为:
 ≤m<1或1<m
≤m<1或1<m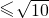
点评:本题给出一个含有对数的绝对值不等式在某个区间上恒成立,求参数m的取值范围,着重考查了对数函数的单调性和绝对值不式的性质等知识,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目