题目内容
在 所在的平面内,点
所在的平面内,点 满足
满足

 ,
, ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
 ,则 ( )
,则 ( )
A. | B. | C. | D. |
C
解析试题分析: ,
,
 四点共线,以AB所在的直线为x轴,以AB的中垂线为y轴,建立直角坐标系,设AB="4," 以AB所在的直线为x轴,以AB的中垂线为y轴,建立直角坐标系,设AB=4,C(a,b),P(x,0),则A(-2,0),B(2,0),
四点共线,以AB所在的直线为x轴,以AB的中垂线为y轴,建立直角坐标系,设AB="4," 以AB所在的直线为x轴,以AB的中垂线为y轴,建立直角坐标系,设AB=4,C(a,b),P(x,0),则A(-2,0),B(2,0), ,∵恒有
,∵恒有
 ,∴
,∴
即  恒成立,∴判别式△
恒成立,∴判别式△ 解得
解得 即点C在AB的垂直平分线上,∴CA=CB,故选C.
即点C在AB的垂直平分线上,∴CA=CB,故选C.
考点:1.向量的数量积;2.正弦定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在四边形ABCD中,下列各式中成立的是( )
A. - - = = | B. + + = = |
C. + + + + = = | D. + + = = + + |
若 ·
· +
+ <0,则△ABC必定是( )
<0,则△ABC必定是( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.等腰直角三角形 |
已知e1,e2是两个单位向量,其夹角为θ,若向量m=2e1+3e2,则|m|=1的充要条件是( )
| A.θ=π | B.θ= |
C.θ= | D.θ= |
已知O是△ABC所在平面内一点,D为BC边中点,且2 +
+ +
+ =0,那么( )
=0,那么( )
A. = = | B. =2 =2 |
C. =3 =3 | D.2 = = |
 ,
, ,定义一种向量积:
,定义一种向量积: .已知向量
.已知向量 ,
, ,点P在
,点P在 的图象上运动,点Q在
的图象上运动,点Q在 的图象上运动,且满足
的图象上运动,且满足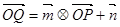 (其中O为坐标原点),则
(其中O为坐标原点),则 上的最大值是( )
上的最大值是( )



 =0,则△AOC的面积为( )
=0,则△AOC的面积为( )



 =2
=2 ,
,  =
=
 +λ
+λ ,则λ等于( )
,则λ等于( )





