题目内容
如图,在四面体ABCD中,△ABD、△ACD、△ABC都全等,且AB=AC=
思路点拨:本题要求二面角,首先根据二面角的平面角的定义构造出对应的二面角的平面角,结合已知条件中出现的线段相等,容易想到添加中点,从而得到相关的垂直关系而达到目的.
解:取BC的中点E,连结AE、DE.
∵AB=AC,∴AE⊥BC.
又△ABD≌△DBC,AB=AC,
∴DB=DC,DE⊥BC.
∴∠AED为二面角ABCD的平面角.
又△ABC≌△DBC,且△ABC是以BC为底的等腰三角形,△DBC也是以BC为底的等腰三角形,所以AB=AC=DB=DC=![]() .
.
又△ABD≌△BDC,∴AD=BC=2.
在Rt△DEB中,DB=![]() ,BE=1,
,BE=1,
∴DE=![]() .
.
同理,AE=![]() .
.
在△AED中,AE=DE=![]() ,AD=2,AD2+DE2=AD2,∠AED=90°,即二面角ABCD的大小为90°.
,AD=2,AD2+DE2=AD2,∠AED=90°,即二面角ABCD的大小为90°.
[一通百通] 有关求二面角的平面角问题的求解,通常考虑根据二面角的平面角的定义构造出相应的平面角,而在构造过程中,往往离不开添加垂线,利用线面垂直、面面垂直关系从而达到目的,最后问题通常转化为解三角形.

练习册系列答案
相关题目
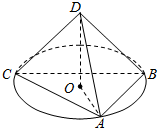 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
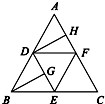 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为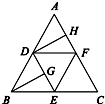 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )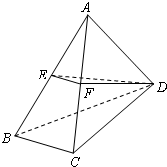 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.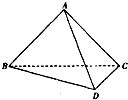 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,