题目内容
底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PA⊥平面ABCD,点E在PD上,且(Ⅰ)求二面角E-AC-D的大小;
(Ⅱ)在棱PC上是否存在一点F,使BF∥平面AEC,若存在,确定点F的位置;若不存在,请说明理由.
解法一:(Ⅰ)作EM⊥AD于M,∵PA⊥面ABCD.
∴面PAD⊥面ABCD

作MN⊥AC于N,连接NE,则NE⊥AC,
∴∠ENM为二面角E-AC-D的平面角,
∵EM=![]() PA=
PA=![]() a,AM=
a,AM=![]() a,
a,
∴MN=AM·sin60°=![]() .
.
∴tanENM=![]() .
.
∴二面角E-AC-D的大小为30°.
(Ⅱ)取PC中点F,PE中点Q,连接FQ、BF、BQ,
设AC∩BD=O,连OE,
则OE∥BQ,QF∥CE,∴平面BQF∥平面ACE,
∴在棱PC上存在中点F,使BF∥平面AEC.
解法二:(1)建立如图所示空间直角坐标系,则A(0,0,0),

B(![]() a,
a,![]() a,0),D(0,a,0),C(
a,0),D(0,a,0),C(![]() a,
a,![]() a,0),P(0,0,a),E(0,
a,0),P(0,0,a),E(0,![]() a,
a,![]() a),
a),
∴![]() =(0,
=(0,![]() a,
a,![]() a),
a),![]() =(
=(![]() a,
a,![]() a,0),
a,0),
设平面ACE的一个法向量为n=(x,y,z),
则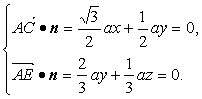 可得n=(
可得n=(![]() ,1),
,1),
而平面ACD的法向量为n1=![]() =(0,0,a),
=(0,0,a),
∴cos<n·n1>=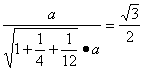 ,
,
∴二面角E-AC-D的大小为30°.
(Ⅱ)由(Ⅰ)![]() =(
=(![]() a,
a,![]() a,-a),
a,-a),
设F为PC上一点,且![]() =
=![]() .
.
又![]() =(
=(![]() a,
a,![]() a,a)
a,a)
∴![]() =(
=(![]() a(λ-1),
a(λ-1),![]() (1+λ)a,a(1-λ)).
(1+λ)a,a(1-λ)).
∴![]() ,
,
∴![]() =λ1(
=λ1(![]() a,
a,![]() a,0)+λ2(0,
a,0)+λ2(0,![]() a,
a,![]() a),
a),
则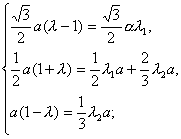 解得
解得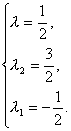
∴当λ=![]() 时,
时,![]() =
=![]()
![]() +
+![]()
![]() ,
,
∴![]() 与
与![]() 共面,此时F为BC中点,
共面,此时F为BC中点,
又BF![]() 平面ACE,∴BF∥平面ACE.
平面ACE,∴BF∥平面ACE.
解法三:(Ⅱ)取PC中点F,由
![]()
=![]()
=![]()
=![]() .
.
∴BF与AE共面, 又BF![]() 平面ACF,∴BF∥平面ACE.
平面ACF,∴BF∥平面ACE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=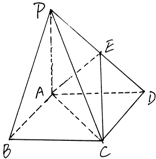 在底面是菱形的四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=60°,PA=AB=2,E是PD中点.
在底面是菱形的四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=60°,PA=AB=2,E是PD中点.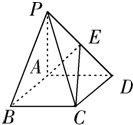 如图,在底面是菱形的四棱锥P-ABCD,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.