Question

【题目】已知 ，且 ．
（1）化简f（a）；
（2）若 ，求 的值．

Answer 1

【答案】
（1）解：∵ ，

∴sinα∈（0，1），cosα∈（0，1），

∴ =cosα +sinα =1﹣sinα+1﹣cosα=2﹣sinα﹣cosα．

（2）解：∵ =2﹣sinα﹣cosα，

∴sinα+cosα= ，

∴两边平方可得：1+2sinαcosα= ，解得：sinαcosα= ，

∴ = = = = ．

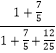【解析】（1）由已知可得sinα∈（0，1），cosα∈（0，1），利用同角三角函数基本关系式化简化简得解．（2）由已知可求sinα+cosα= ，两边平方可得sinαcosα= ，将所求通分后化简即可计算得解．
【考点精析】关于本题考查的同角三角函数基本关系的运用，需要了解同角三角函数的基本关系：；;（3） 倒数关系：才能得出正确答案．