题目内容

若a、b∈R，且4≤a²+b²≤9，则a²-ab+b²的最大值与最小值之和是________．

$\text{[math]}$
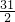
分析：先推出-（a²+b²）≤2ab≤a²+b²，结合条件解可得ab的范围，又由不等式的可加性求出a²-ab+b²的范围，再求出最大值与最小值之和．
解答：∵（a+b）²≥0或（a-b）²≥0，∴-（a²+b²）≤2ab≤a²+b²，
∵4≤a²+b²≤9，进而可得-9≤2ab≤4，
解可得，- $\text{[math]}$ ≤ab≤2，∴-2≤-ab≤ $\text{[math]}$ ，
∴-2+4≤a²-ab+b²≤ $\text{[math]}$ +9，即2≤a²-ab+b²≤ $\text{[math]}$
∴所求的最大值与最小值之和是：2+ $\text{[math]}$ = $\text{[math]}$ ，
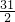故答案为： $\text{[math]}$ ．
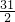点评：本题考查不等式的基本性质与运用，需要给出-（a²+b²）≤2ab≤a²+b²的证明过程，解题时要注意把握题中的条件．