题目内容
若数列 满足
满足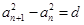 ,其中
,其中 为常数,则称数列
为常数,则称数列 为等方差数列,已知等方差数列
为等方差数列,已知等方差数列 满足
满足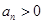 ,
,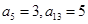 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前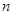 项和;
项和;
(3)记 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的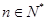 恒成立?请说明理由。
恒成立?请说明理由。
【答案】
(1)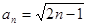 ;(2)
;(2)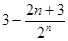 ;(3)当
;(3)当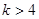 时,不等式
时,不等式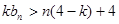 对于一切的
对于一切的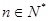 恒成立 .
恒成立 .
【解析】本试题主要考查了数列的概念和灵活运用新的定义,解决数列的通项公式和求和问题,以及不等式的恒成立问题的综合运用
(1)利用新定义可得由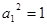 ,
, 得,
得,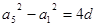 ,∴
,∴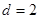
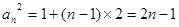
(2)中结合上一问的结论得到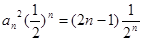 ,然后利用错位相减法得到求和
,然后利用错位相减法得到求和
(3)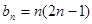 ,不等式
,不等式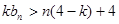 恒成立,
恒成立,
即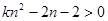 对于一切的
对于一切的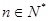 恒成立。
恒成立。
∴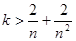
分离参数的思想求解k的取值范围。
解:(Ⅰ)由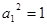 ,
, 得,
得,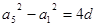 ,∴
,∴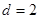
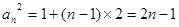 ,
,
∵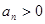 ,∴
,∴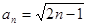
数列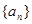 的通项公式为
的通项公式为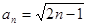 ;
;
(Ⅱ)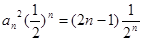
设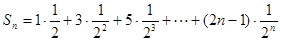 ①
①
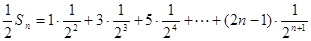 ②
②
①-②,得
∴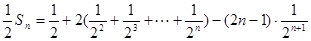
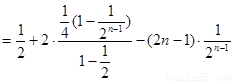
∴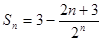
即数列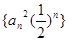 的前
的前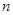 项和为
项和为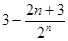
(Ⅲ)解法1: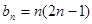 ,不等式
,不等式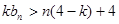 恒成立,
恒成立,
即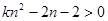 对于一切的
对于一切的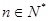 恒成立。
恒成立。
设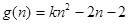 ,当
,当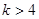 时,由于对称轴
时,由于对称轴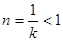 ,且
,且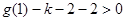
而函数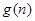 在
在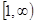 是增函数,∴不等式
是增函数,∴不等式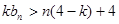 恒成立,
恒成立,
即当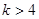 时,不等式
时,不等式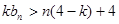 对于一切的
对于一切的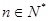 恒成立
恒成立
解法2: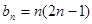 ,不等式
,不等式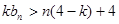 恒成立,即
恒成立,即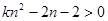 对于一切的
对于一切的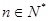 恒成立。
恒成立。
∴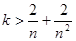
∵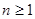 ,∴
,∴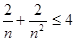 .而
.而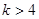
∴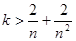 恒成立.
恒成立.
故当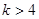 时,不等式
时,不等式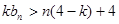 对于一切的
对于一切的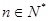 恒成立.
恒成立.

练习册系列答案
相关题目
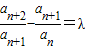 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列. (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.