Question

 已知函数．

（Ⅰ）求函数的单调区间；

（Ⅱ）设，若对任意，，不等式 恒成立，求实数的取值范围．

Answer 1

解： （I）的定义域是         ．．．．．．．．．．．1分

                      ．．．．．．．．．．．．．．． 2分

由及 得；由及得，

故函数的单调递增区间是；单调递减区间是     ．．．．．．．．4分

（II）若对任意，，不等式恒成立，

问题等价于，                   ．．．．．．．．．5分

由（I）可知，在上，是函数极小值点，这个极小值是唯一的极值点，

故也是最小值点，所以；                  ．．．．．．．．．．．．．．．．．．．6分

当时，；

当时，；

当时，；             ．．．．．．．．．．．．8分

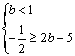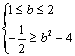问题等价于 或 或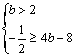            ．．．．．．．．11分

       解得 或 或

       即，所以实数的取值范围是      ．．．．．．．．．．．．．．．．．12分