Question

7．如图，平行六面体体ABCD-A₁B₁C₁D₁中，所有棱长均为1，且∠BAD=∠A₁AB=∠A₁AC=60°．
（Ⅰ）求证：平面A₁BD⊥平面A₁ACC₁；
（Ⅱ）求四棱锥A₁-BB₁D₁D的体积．

Answer 1

分析 （Ⅰ）连接AC、BD、A₁B、A₁D，AC与BD相交于一点O，连接A₁O，证明BD⊥平面A₁ACC₁，然后证明平面A₁BD⊥平面A₁ACC₁；
（Ⅱ）说明四棱锥A₁-BB₁D₁D为正四棱锥，求出A₁到平面BB₁D₁D的距离，底面${S}_{{BB}_{1}{D}_{1}D}=1×1=1$，然后求解体积．

解答 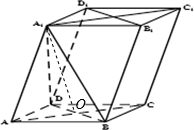（Ⅰ）证明：连接AC、BD、A₁B、A₁D，AC与BD相交于一点O，连接A₁O，
因为平行六面体ABCD-A₁B₁C₁D₁中，所有棱长均为1，
所以AC⊥BD，且O为BD中点，∠BAD=∠A₁AB=∠A₁AD=60°，
所以A₁B=A₁D=BD，所A₁O⊥BD，A₁O∩A₁C=O，
所以BD⊥平面A₁ACC₁，BD?平面A₁BD，
所以平面A₁BD⊥平面A₁ACC₁；
（Ⅱ）解：由（Ⅰ）知A₁A⊥BD，又A₁A∥B₁B，所以B₁B⊥BD，
四棱锥A₁-BB₁D₁D为正四棱锥，V=$\frac{1}{3}$${S}_{{BB}_{1}{D}_{1}D}$•h，h为A₁到平面BB₁D₁D的距离，h=$\sqrt{（\frac{\sqrt{3}}{2}）^{2}-{（\frac{1}{2}）}^{2}}$=$\frac{\sqrt{2}}{2}$，${S}_{{BB}_{1}{D}_{1}D}=1×1=1$，
∴$V=\frac{{\sqrt{2}}}{6}$．

点评 本题考查几何体的体积的求法，平面与平面垂直的判定定理的应用，考查逻辑推理能力以及计算能力．