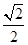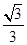题目内容
(本小题满分14分)
已知椭圆C: +
+ =1
=1 的左.右焦点为
的左.右焦点为 ,离心率为
,离心率为 ,直线
,直线 与x轴、y轴分别交于点
与x轴、y轴分别交于点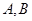 ,
, 是直线
是直线 与椭圆C的一个公共点,
与椭圆C的一个公共点, 是点
是点 关于直线
关于直线 的对称点,设
的对称点,设 =
=
(Ⅰ)证明: ; (Ⅱ)确定
; (Ⅱ)确定 的值,使得
的值,使得 是等腰三角形.
是等腰三角形.
已知椭圆C:
 +
+ =1
=1 的左.右焦点为
的左.右焦点为 ,离心率为
,离心率为 ,直线
,直线 与x轴、y轴分别交于点
与x轴、y轴分别交于点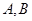 ,
, 是直线
是直线 与椭圆C的一个公共点,
与椭圆C的一个公共点, 是点
是点 关于直线
关于直线 的对称点,设
的对称点,设 =
=
(Ⅰ)证明:
 ; (Ⅱ)确定
; (Ⅱ)确定 的值,使得
的值,使得 是等腰三角形.
是等腰三角形.解:(Ⅰ)因为
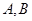 分别是直线
分别是直线 与x轴、y轴的交点,所以
与x轴、y轴的交点,所以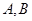 的坐标分别是
的坐标分别是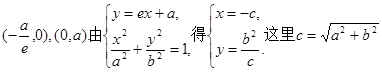 .
.所以点
 的坐标是(
的坐标是(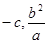 ). 由
). 由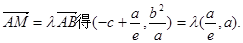
即
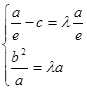 ,得
,得
(Ⅱ)由
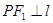 ,得
,得 为钝角,要使
为钝角,要使 为等腰三角形,必有
为等腰三角形,必有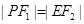 ,即
,即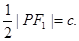
设点
 到
到 的距离为
的距离为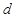 ,由
,由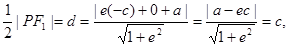
得
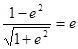 所以
所以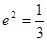 ,于是
,于是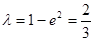
即当
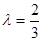 时,
时, 为等腰三角形
为等腰三角形略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
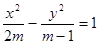 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线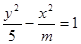 的离心率
的离心率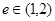 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。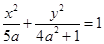 的焦点在
的焦点在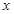 轴上,则它的离心率的取值范围为( )
轴上,则它的离心率的取值范围为( )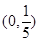
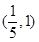
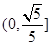
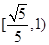
 =
= ,长轴的左右两个端点分别为
,长轴的左右两个端点分别为
 ;
; 在该椭圆上,且
在该椭圆上,且 ,求点
,求点 轴的距离;
轴的距离;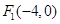 ,
,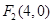 ,P在椭圆上,若 △
,P在椭圆上,若 △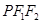 的面积的最大值为12,则椭圆方程为
的面积的最大值为12,则椭圆方程为



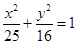 上任意一点,
上任意一点,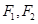 为左、右焦点,
为左、右焦点, 如图所示.
如图所示.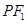 的中点为
的中点为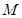 ,求证:
,求证: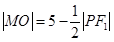
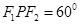 ,求|PF1|·|PF2|之值;
,求|PF1|·|PF2|之值;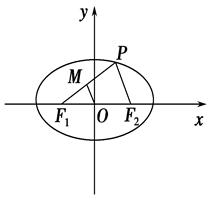
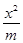 + y2=1(m>1)和双曲线
+ y2=1(m>1)和双曲线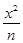 - y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( )
- y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( ) 的左、右顶点分别为
的左、右顶点分别为 ,椭圆
,椭圆 的右焦点为
的右焦点为 ,过
,过 轴的直线与椭圆相交于
轴的直线与椭圆相交于 ,若线段
,若线段 的长为
的长为 。
。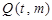 是直线
是直线 上的点,直线
上的点,直线 与椭圆
与椭圆 ,求证:直线
,求证:直线 必过
必过 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )