题目内容
(1)求证:平面
 平面
平面 ;
;(2)求正方形的边长;
(3)求二面角
 的平面角的正切值.
的平面角的正切值.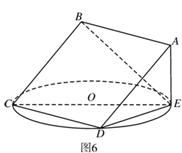
(1)略
(2)

(3)

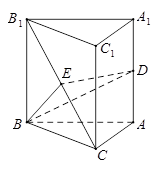
(1)证明:∵ 垂直于圆
垂直于圆 所在平面,
所在平面, 在圆
在圆 所在平面上,
所在平面上,


∴
 .
.
在正方形 中,
中, ,
,
∵ ,∴
,∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴平面 平面
平面 . ……… 4分
. ……… 4分
 (2)∵
(2)∵ 平面
平面 ,
, 平面
平面 ,
,
∴.
∴为圆 的直径,即
的直径,即 .
.
设正方形
 的边长为
的边长为 ,
,
在 △
△ 中,
中, ,
,
在 △
△ 中,
中, ,
,
由 ,解得,
,解得, . ……… 8分
. ……… 8分
(3). 过点 作
作 于点
于点 ,作
,作 交
交 于点
于点 ,连结
,连结 ,
,
由于 平面
平面 ,
, 平面
平面 ,
,
∴ .∵
.∵ ,
,
∴ 平面
平面 .∵
.∵ 平面
平面 ,∴
,∴ .
.
∵ ,
, ,∴
,∴ 平面
平面 .
.
∵ 平面
平面 ,∴
,∴ .
.
∴ 是二面角
是二面角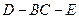 的平面角. ……………… 10分
的平面角. ……………… 10分
在 △
△ 中,
中, ,
, ,
,
∵ ,∴
,∴ .
.
在 △
△ 中,
中, ,∴
,∴ .
.
故二面角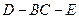 的平面角的正切值为
的平面角的正切值为 . ………………12分
. ………………12分
 垂直于圆
垂直于圆 所在平面,
所在平面, 在圆
在圆 所在平面上,
所在平面上,

∴

 .
. 在正方形
 中,
中, ,
,
∵
 ,∴
,∴ 平面
平面 .
.∵
 平面
平面 ,
,∴平面
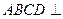 平面
平面 . ……… 4分
. ……… 4分 (2)∵
(2)∵ 平面
平面 ,
, 平面
平面 ,
, ∴.
∴为圆
 的直径,即
的直径,即 .
.设正方形

 的边长为
的边长为 ,
,在
 △
△ 中,
中, ,
,在
 △
△ 中,
中, ,
,由
 ,解得,
,解得, . ……… 8分
. ……… 8分(3). 过点
 作
作 于点
于点 ,作
,作 交
交 于点
于点 ,连结
,连结 ,
,由于
 平面
平面 ,
, 平面
平面 ,
,∴
 .∵
.∵ ,
,∴
 平面
平面 .∵
.∵ 平面
平面 ,∴
,∴ .
.∵
 ,
, ,∴
,∴ 平面
平面 .
.∵
 平面
平面 ,∴
,∴ .
.∴
 是二面角
是二面角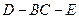 的平面角. ……………… 10分
的平面角. ……………… 10分在
 △
△ 中,
中, ,
, ,
,
∵
 ,∴
,∴ .
. 在
 △
△ 中,
中, ,∴
,∴ .
.故二面角
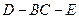 的平面角的正切值为
的平面角的正切值为 . ………………12分
. ………………12分
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 的边长为4,
的边长为4, 是
是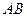 边上的高,
边上的高, 分别是
分别是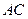 和
和 边的中点,现将△
边的中点,现将△ .
. 的位置关系,并说明理由;
的位置关系,并说明理由; 的余弦值;
的余弦值; ,使
,使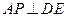 ?证明你的结论.
?证明你的结论.
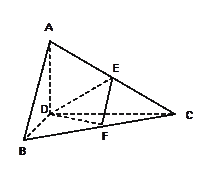
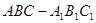 中,
中,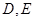 分别为
分别为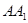 ,
,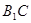 的中点.
的中点.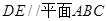 ;
; 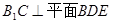 .
.


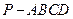 的底面
的底面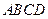 为正方形,
为正方形,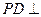 平面
平面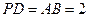 ,
,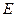
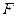 ,
,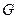 分别为
分别为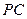 ,
,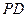 和
和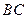 的中点. (1)求证
的中点. (1)求证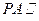 平面
平面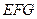 .(2)求异面直线
.(2)求异面直线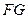 与
与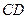 所成角的正切值.
所成角的正切值.
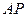 是⊙
是⊙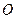 的切线,
的切线, 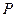 为切点,
为切点,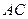 是⊙O的割线,与⊙
是⊙O的割线,与⊙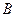 ,
,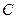 两点,圆心
两点,圆心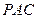 的内部,点
的内部,点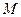 是
是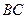 的中点.
的中点.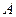 ,
, 的大小.
的大小.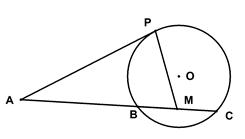
 .
.