题目内容
在某次测验中,有6位同学的平均成绩为75分。用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率。

解:(1)
 ………………3分
………………3分
 ,
, ………………6分
………………6分
(2)从5位同学中随机选取2位同学,共有如下10种不同的取法:
{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5} ,
,
选出的2位同学中,恰有1位同学的成绩位于(68,75)的取 法共有如下4种取法:
法共有如下4种取法:
{1,2},{2,3},{2,4},{2,5},故所求概率为 ………………12分
………………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ”的否定是( )
”的否定是( )
 .不存
.不存 在
在 .存在
.存在
 .对任意的
.对任意的
 .对任意的
.对任意的
 游纪念
游纪念 品,每件产品的成本是
品,每件产品的成本是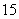 元,销售价是
元,销售价是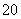 元,月平均销售
元,月平均销售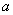 件.通过改进工艺,产品的成本不变,质量和技术
件.通过改进工艺,产品的成本不变,质量和技术 含金量提高,市场分析的结果表明,如果产
含金量提高,市场分析的结果表明,如果产 品的销售价提高的百分率为
品的销售价提高的百分率为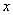
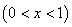 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为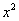 .记改进工
.记改进工 艺后,旅游部门销售该纪念品的月平均利润是
艺后,旅游部门销售该纪念品的月平均利润是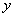 (元).
(元). 表示
表示 ,
, 两者中的较小者,若函数
两者中的较小者,若函数 ,则满足
,则满足 的
的 的取值范围是( )
的取值范围是( )  B.
B.  C.
C.  D.
D. 
 上一点p到椭圆一个焦点的距离3,则点p到另一个焦点的距离为( )
上一点p到椭圆一个焦点的距离3,则点p到另一个焦点的距离为( )
 表示双曲线,则
表示双曲线,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. 作垂直于实轴
作垂直于实轴 的直线,交双曲线于P、Q,
的直线,交双曲线于P、Q, 是另一焦点,若∠
是另一焦点,若∠ ,则双曲线的离心率
,则双曲线的离心率 等于( )
等于( )
 B
B C
C D
D
 上的函数
上的函数 ,对任意
,对任意 ,都有
,都有 成立,若函数
成立,若函数 的图象关于点
的图象关于点 对称,则
对称,则 =( )
=( )