题目内容
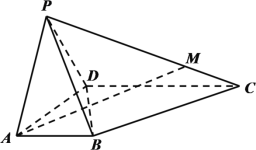
【题目】如图，在三棱锥
中，
平面ABC，平面
平面PBC，
，
．
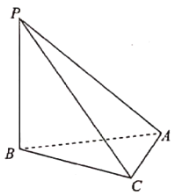
（1）证明：
平面PBC；
（2）求点C到平面PBA的距离．
【答案】（1）证明见解析；（2）
．
【解析】
（1）由
平面ABC，可得
，通过取
中点
，由平面
平面PBC，可得
平面PAC，从而
，然后根据线面垂直的判定定理即可证得
平面PBC；
（2）根据平面ABC可得平面
平面ABC，过点过点C作
，交AB于M，则
即为所求，在
内根据等面积法即可求出．
（1）证明：
平面ABC，
平面ABC，
．
取PC的中点D，连接BD，
，
．
又
平面平面PBC，平面
平面
，
平面PBC，
平面PAC．又平面PAC，
．
，
平面PBC．
（2）易知平面平面ABC，AB为交线，在
中，过点C作，交AB于M，则
平面PBA．
又
，
，
点C到平面PBA的距离为．
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后，下一代颠覆性的核心技术区块链作为构造信任的机器，将可能彻底改变整个人类社会价值传递的方式，2015年至2019年五年期间，中国的区块链企业数量逐年增长，居世界前列现收集我国近5年区块链企业总数量相关数据，如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y（单位：千个） | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注：参考数据
（其中z＝lny）．
附：样本（xi，yi）（i＝1，2，…，n）的最小二乘法估计公式为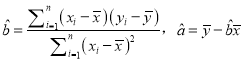
（1）根据表中数据判断，y＝a+bx与y＝cedx（其中e＝2.71828…，为自然对数的底数），哪一个回归方程类型适宜预测未来几年我国区块链企业总数量？（给出结果即可，不必说明理由）
（2）根据（1）的结果，求y关于x的回归方程（结果精确到小数点后第三位）；
（3）为了促进公司间的合作与发展，区块链联合总部决定进行一次信息化技术比赛，邀请甲、乙、丙三家区块链公司参赛比赛规则如下：①每场比赛有两个公司参加，并决出胜负；②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛；③在比赛中，若有一个公司首先获胜两场，则本次比赛结束，该公司就获得此次信息化比赛的“优胜公司”，已知在每场比赛中，甲胜乙的概率为
，甲胜丙的概率为
，乙胜丙的概率为
，请通过计算说明，哪两个公司进行首场比赛时，甲公司获得“优胜公司”的概率最大？
【题目】某城市208年抽样100户居民的月均用电量（单位：千瓦时），以
，
，
，
，
，
，
分组，得到如下频率分布表：
分组 | 频数 | 频率 |
|
| 0.04 |
| 19 |
|
|
| 0.22 |
| 25 | 0.25 |
| 15 | 0.15 |
| 10 |
|
| 5 | 0.05 |
（1）求表中
的值，并估计2018年该市居民月均用电量的中位数
；
（2）该城市最近十年的居民月均用电量逐年上升，以当年居民月均用电量的中位数
（单位：千瓦时）作为统计数据，下图是部分数据的折线图．
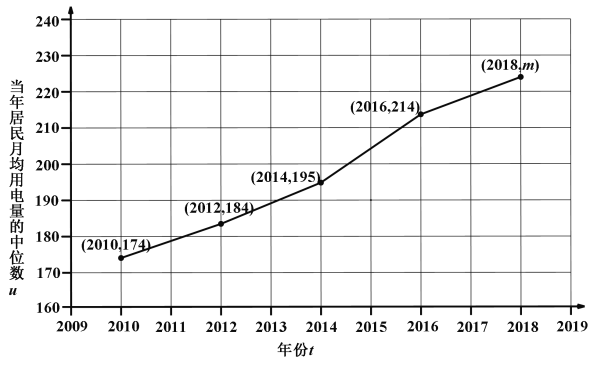
由折线图看出，可用线性回归模型拟合与年份
的关系．
①为简化运算，对以上数据进行预处理，令
，
，请你在答题卡上完成数据预处理表；
②建立关于的线性回归方程，预测2020年该市居民月均用电量的中位数．
附：回归直线
的斜率和截距的最小二乘估计公式分别为：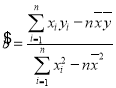
，
．
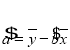