Question

11．定义在R上的奇函数f（x）满足f（x+2）=-f（x），且在[-1，0]上是增函数，给出下面关于f（x）的判断：①f（x）的图象关于直线x=1的对称；②f（x）在[1，2]上是减函数；③f（2）=f（0）．其中正确判断的序号为①②③（写出所有正确判断的序号）．

Answer 1

分析 根据已知分析出函数的图象和性质，画出函数的草图，数形结合，可得答案．

解答 解：∵函数f（x）满足f（x+2）=-f（x），
∴f（x+4）=f[（x+2）+2]=-f（x+2）=f（x），
即函数f（x）是以4为周期的周期函数，
又由函数f（x）为定义在R上的奇函数，且在[-1，0]上是增函数，
故函数f（x）的图象如下图所示：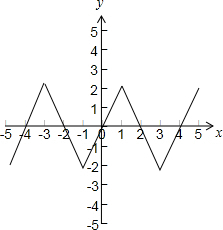

由图可得：
①f（x）的图象关于直线x=1的对称，正确；
②f（x）在[1，2]上是减函数，正确；
③f（2）=f（0）=0，正确．
故正确的命题的序号为：①②③，
故答案为：①②③

点评 本题以命题的真假判断与应用为载体，考查了函数的图象和性质，难度中档．