题目内容
已知△ABC所在平面与直角梯形ACEF所在平面垂直,AF⊥AC,EB⊥AB,AF∥CE,AB=BC=CE=2AF=2,O为AC中点.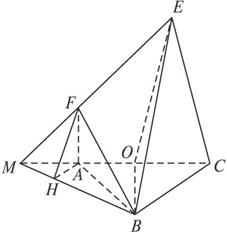
(1)求证:面OBE⊥面ACEF;
(2)求面EFB与面ABC所成二面角的大小.
(1)证明:在△ABC中,AB=BC,O为AC中点,
∴OB⊥AC.
∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,OB![]() 平面ABC,
平面ABC,
∴OB⊥平面ACEF.又OB![]() 面OBE,
面OBE,
∴面OBE⊥面ACEF.

(2)解:延长EF交CA的延长线于点M,连结BM,
则面EFB∩面ABC=BM.
作AH⊥BM于点H,连结FH,
∵平面ABC⊥平面ACEF,
且平面ABC∩平面ACEF=AC,AF⊥AC,
∴AF⊥平面ABC.
由三垂线定理得FH⊥BM,
因此,∠FAH为面EFB与面ABC所成二面角的平面角.
∵AF∥CE,AF⊥平面ABC,
∴CE⊥平面ABC.
又EB⊥AB,由三垂线定理的逆定理得BC⊥AB,
∵AF=1,且A为CM中点,
在△MBO中,MO=3![]() ,OB=
,OB=![]() ,
,
∴MB=![]() =2
=2![]() .
.
又Rt△MAH∽Rt△MBO,
∴![]() ,
,
即AH=![]() .
.
在△FAH中,tan∠FHA=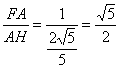 ,
,
面EFB与面ABC所成二面角的大小为arctan![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知△ABC所在平面上的动点M满足2
•
=
2 -
2,则M点的轨迹过△ABC的( )
| AM |
| BC |
| AC |
| AB |
| A、内心 | B、垂心 | C、重心 | D、外心 |