题目内容
甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令ξ为本场比赛的局数,求ξ的概率分布和数学期望.(精确到0.000 1)
解:单局比赛甲队胜乙队的概率为0.6,乙队胜甲队的概率为1-0.6=0.4.
比赛3局结束有两种情况:甲队胜3局或乙队胜3局,因而
P(ξ=3)=0.63+0.43=0.28.
比赛4局结束有两种情况:前3局中甲队胜2局,第4局甲队胜;或前3局中乙队胜2局,第4局乙队胜,因而
P(ξ=4)=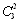 ×0.62×0.4×0.6+
×0.62×0.4×0.6+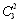 ×0.42×0.6×0.4=0.374 4.
×0.42×0.6×0.4=0.374 4.
比赛5局结束有两种情况:前4局中甲队胜2局、乙队胜2局,第五局甲胜或乙胜,因而
P(ξ=5)=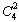 ×0.62×0.42×0.6+
×0.62×0.42×0.6+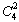 ×0.62×0.42×0.4=0.345 6.
×0.62×0.42×0.4=0.345 6.
所以ξ的概率分布为
ξ | 3 | 4 | 5 |
P | 0.28 | 0.374 4 | 0.345 6 |
ξ的期望Eξ=3×P(ξ=3)+4×P(ξ=4)+5×P(ξ=5)=3×0.28+4×0.374 4+5×0.345 6=4.065 6.

练习册系列答案
相关题目
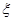 表示本场比赛的局数,则
表示本场比赛的局数,则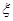 为本场比赛的局数.求
为本场比赛的局数.求