题目内容
设函数 .
.
(Ⅰ)求 的最小值,并求使
的最小值,并求使 取得最小值的
取得最小值的 的集合;
的集合;
(Ⅱ)不画图,说明函数 的图像可由
的图像可由 的图象经过怎样的变化得到.
的图象经过怎样的变化得到.
【答案】
(Ⅰ) 的最小值为
的最小值为 ,此时x的集合
,此时x的集合 (Ⅱ)见解析
(Ⅱ)见解析
【解析】(1)


当 时,
时, ,此时
,此时
所以, 的最小值为
的最小值为 ,此时x的集合
,此时x的集合 .
.
 横坐标不变,纵坐标变为原来的
横坐标不变,纵坐标变为原来的 倍,得
倍,得 ;
;
然后 向左平移
向左平移 个单位,得
个单位,得
(1)利用两角的和差公式,辅助角公式将三角函数化成 ,若
,若 时,当
时,当 时取最小值;(2)要熟练平移变换,伸缩变换.
时取最小值;(2)要熟练平移变换,伸缩变换.
【考点定位】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目









 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。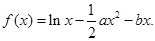
 时,求
时,求 的最大值;
的最大值; ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤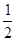 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, 的最小正周期以及单调增区间;
的最小正周期以及单调增区间; 时,求
时,求 ,求
,求 的值.
的值. 。
。 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;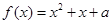 在区间[0, 2] 恰有两个不等实根,求a的取值范围。
在区间[0, 2] 恰有两个不等实根,求a的取值范围。