题目内容
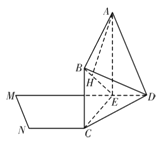
【题目】如图,等腰梯形MNCD中,MD∥NC,MN=![]() MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC
MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC

(1)求证:DE⊥平面ABCE;
(2)求点A到平面DBE的距离
【答案】(1)见解析(2)![]()
【解析】
(1)等腰梯形中,MD=4,CD=MN=2,利用余弦定理求出![]() ,由勾股定理得到CE
,由勾股定理得到CE![]() DE,然后得到AE⊥平面CED,所以
DE,然后得到AE⊥平面CED,所以![]() ,从而可以得到DE⊥平面ABCE.(2)
,从而可以得到DE⊥平面ABCE.(2)
由(1)得到的CE⊥AE,可求出![]() 的面积,由DE⊥平面ABCE,求出三棱锥
的面积,由DE⊥平面ABCE,求出三棱锥![]() 的体积,利用勾股定理得到
的体积,利用勾股定理得到![]() 的长,然后求出
的长,然后求出![]() 的面积,利用等体积转化,求出点A到平面DBE的距离.
的面积,利用等体积转化,求出点A到平面DBE的距离.
(1)等腰梯形MNCD中,MD∥NC,CD=![]() MD=2
MD=2
∴MD=4,CD=MN=2,
△CED中,∠CDE=60°,ED=MD-EM=1,
则由余弦定理![]()
∴CE![]() ,∴CE2+ED2=CD2
,∴CE2+ED2=CD2
∴CE![]() DE,∴CE
DE,∴CE![]() ME,CE
ME,CE![]() AE
AE
又AE⊥DC,DC![]() CE=C,
CE=C,
∴AE⊥平面CED
而![]() 平面CED
平面CED
∴![]() ,又
,又![]() ,AE
,AE![]() CF=E
CF=E
∴DE⊥平面ABCE
(2)由(1)因CE⊥AE,则![]()
因DE⊥平面ABCE,则![]()
等腰梯形MCD中MD∥NC,MD=4,
CD=MN=2,CE⊥DE,DE=1
则NC=MD-2DE=2,故BC=2,
![]()
设点A到平面DBE的距离为h,因DE⊥平面ABCE
则![]() ,得h=
,得h=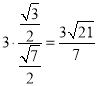
所以点A到平面DBE的距离为![]()

练习册系列答案
相关题目