题目内容
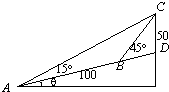如图，在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°，向山顶前进100m后，又从点B测得斜度为45°，假设建筑物高50m，设山对于地平面的斜度θ，则cosθ=| 3 |
| 3 |
分析：在△ABC中，利用正弦定理，先计算BC，再在△DBC中，利用正弦定理，可求cosθ的值．
解答：解：在△ABC中，AB=100m，∠CAB=15°，∠ACB=45°-15°=30°
由正弦定理：
=
，可得BC=200sin15°
在△DBC中，CD=50m，∠CBD=45°，∠CDB=90°+θ
由正弦定理：
=
∴cosθ=2
sin15°=
-1．
故答案为：
-1
由正弦定理：
| 100 |
| sin30° |
| BC |
| sin15° |
在△DBC中，CD=50m，∠CBD=45°，∠CDB=90°+θ
由正弦定理：
| 50 |
| sin45° |
| 200sin15° |
| sin(90°+θ) |
∴cosθ=2
| 2 |
| 3 |
故答案为：
| 3 |
点评：本题考查正弦定理的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
如图，在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°，向山顶前进100m后，又从点B测得斜度为45°，假设建筑物高50m，设山对于地平面的斜度θ，求cosθ的值．
.
