题目内容
 如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度θ,求cosθ的值.
如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度θ,求cosθ的值.分析:在三角形ABC中,由∠CBD-∠CAB求出∠ACB的度数,再由AB的长,以及sin∠CAB与sin∠ACB的值,利用正弦定理表示出BC,在三角形DBC中,由由CD,∠CBD=45°与∠CDB=90°+θ,利用正弦定理列出关系式,将各自的值代入利用诱导公式化简,即可求出cosθ的值.
解答:解:在△ABC中,AB=100m,∠CAB=15°,∠ACB=45°-15°=30°,
∴由正弦定理得:
=
,
解得:BC=200sin15°(m),
在△DBC中,CD=50m,∠CBD=45°,∠CDB=90°+θ,
sin15°=sin(45°-30°)=
×
-
×
=
,
∴由正弦定理得:
=
,
解得:sin(90°+θ)=cosθ=
=
-1.
∴由正弦定理得:
| 100 |
| sin30° |
| BC |
| sin15° |
解得:BC=200sin15°(m),
在△DBC中,CD=50m,∠CBD=45°,∠CDB=90°+θ,
sin15°=sin(45°-30°)=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 4 |
∴由正弦定理得:
| 50 |
| sin45° |
| 200sin15° |
| sin(90°+θ) |
解得:sin(90°+θ)=cosθ=
| 200sin15°sin45° |
| 50 |
| 3 |
点评:此题考查了正弦定理,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
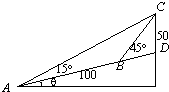 如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度θ,则cosθ=
如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度θ,则cosθ=

