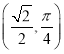题目内容
【题目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,________.是否存在以
,________.是否存在以![]() ,
,![]() ,
,![]() 为边的三角形?如果存在,求出
为边的三角形?如果存在,求出![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
从①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
【答案】详见解析
【解析】
若选取条件①![]() ,可先求出
,可先求出![]() 的值,进而由余弦定理
的值,进而由余弦定理![]() ,可出
,可出![]() 的值,进而结合
的值,进而结合![]() ,可求出
,可求出![]() 的值,从而可判断该三角形存在,进而求出三角形的面积即可;
的值,从而可判断该三角形存在,进而求出三角形的面积即可;
若选取条件②,由余弦定理![]() ,可出
,可出![]() 的值,进而结合
的值,进而结合![]() ,可求得
,可求得![]() ,从而可知该三角形不存在;
,从而可知该三角形不存在;
若选取条件③![]() ,可得
,可得![]() ,进而分两种情况,分别讨论即可.
,进而分两种情况,分别讨论即可.
若选取条件①![]() ,此时
,此时![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
则![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,解得
,解得![]() 或者
或者![]() ,
,
所以存在以![]() ,
,![]() ,
,![]() 为边的三角形,其面积为
为边的三角形,其面积为![]() .
.
若选取条件②![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
则![]() ,所以
,所以![]() ,显然不成立,所以不存在以
,显然不成立,所以不存在以![]() ,
,![]() ,
,![]() 为边的三角形.
为边的三角形.
若选取条件③![]() ,得
,得![]() ,
,
由选取条件①可知,当![]() 时,存在以
时,存在以![]() ,
,![]() ,
,![]() 为边的三角形,其面积为
为边的三角形,其面积为![]() .
.
由选取条件②可知,当![]() 时,不存在以
时,不存在以![]() ,
,![]() ,
,![]() 为边的三角形.
为边的三角形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目