题目内容
已知x轴上的点A1,A2…,An满足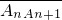 =
=
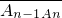 (n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|
(n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|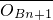 |=|
|=|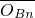 |+2
|+2 (n∈N*),其中B1(3,3).
(n∈N*),其中B1(3,3).
(1)用n表示点An与Bn的坐标;
(2)设直线AnBn的斜率为kn,求 kn的值;
kn的值;
(3)求四边形AnAn+1Bn+1Bn面积S的取值范围.
解:(1)由题意,
∵A1(1,0),A2(5,0),∴x2-x1=4
∴{xn-xn-1}是以4为首项, 为公比的等比数列
为公比的等比数列
∴
∴xn=x1+(x2-x1)+…+(xn-xn-1)=1+4+…+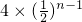 =9-24-n
=9-24-n
∴An(9-24-n,0);
∵射线y=x(x≥0)上,满足|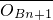 |=|
|=|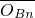 |+2
|+2 (n∈N*),
(n∈N*),
∴ xn+1=
xn+1=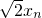 +2
+2
∴xn+1-xn=2
∵B1(3,3).
∴{xn}是以3为首项,2为公差的等差数列,
∴xn=2n+1
∴Bn(2n+1,2n+1);
(2)设直线AnBn的斜率为kn= ,∴
,∴ kn=
kn= =1;
=1;
(3)四边形AnAn+1Bn+1Bn面积S= (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
=
设an= ,则an+1=
,则an+1=
∵an+1-an=[ ]-[
]-[ ]=
]=
∴a2>a1,a2>a3>a4>a5>…
∴a2最大,为12
∴四边形AnAn+1Bn+1Bn面积S的取值范围为(-∞,12].
分析:(1)根据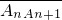 =
=
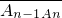 ,可得
,可得 ,从而可得{xn-xn-1}是以4为首项,
,从而可得{xn-xn-1}是以4为首项, 为公比的等比数列;利用射线y=x(x≥0)上,满足|
为公比的等比数列;利用射线y=x(x≥0)上,满足|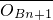 |=|
|=|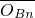 |+2
|+2 (n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标;
(n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标;
(2)确定直线AnBn的斜率为kn= ,从而可求
,从而可求 kn的值;
kn的值;
(3)四边形AnAn+1Bn+1Bn面积S= (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
= ,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.
,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.
点评:本题考查数列的证明,考查数列通项的求解,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

∵A1(1,0),A2(5,0),∴x2-x1=4
∴{xn-xn-1}是以4为首项,
 为公比的等比数列
为公比的等比数列∴

∴xn=x1+(x2-x1)+…+(xn-xn-1)=1+4+…+
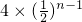 =9-24-n
=9-24-n∴An(9-24-n,0);
∵射线y=x(x≥0)上,满足|
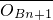 |=|
|=|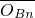 |+2
|+2 (n∈N*),
(n∈N*),∴
 xn+1=
xn+1=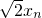 +2
+2
∴xn+1-xn=2
∵B1(3,3).
∴{xn}是以3为首项,2为公差的等差数列,
∴xn=2n+1
∴Bn(2n+1,2n+1);
(2)设直线AnBn的斜率为kn=
 ,∴
,∴ kn=
kn= =1;
=1;(3)四边形AnAn+1Bn+1Bn面积S=
 (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
=
设an=
 ,则an+1=
,则an+1=
∵an+1-an=[
 ]-[
]-[ ]=
]=
∴a2>a1,a2>a3>a4>a5>…
∴a2最大,为12
∴四边形AnAn+1Bn+1Bn面积S的取值范围为(-∞,12].
分析:(1)根据
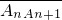 =
=
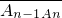 ,可得
,可得 ,从而可得{xn-xn-1}是以4为首项,
,从而可得{xn-xn-1}是以4为首项, 为公比的等比数列;利用射线y=x(x≥0)上,满足|
为公比的等比数列;利用射线y=x(x≥0)上,满足|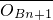 |=|
|=|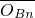 |+2
|+2 (n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标;
(n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标;(2)确定直线AnBn的斜率为kn=
 ,从而可求
,从而可求 kn的值;
kn的值;(3)四边形AnAn+1Bn+1Bn面积S=
 (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
= ,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.
,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.点评:本题考查数列的证明,考查数列通项的求解,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 =
=
 (n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|
(n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|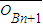 |=|
|=|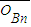 |+2
|+2 (n∈N*),其中B1(3,3).
(n∈N*),其中B1(3,3).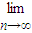 kn的值;
kn的值;