题目内容
已知数列 的通项公式
的通项公式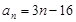 ,则数列
,则数列 的前
的前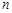 项和
项和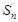 取得最小值时
取得最小值时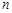 的值为( )
的值为( )
A. | B.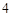 | C.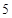 | D.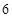 |
C
解析试题分析:根据 时,数列
时,数列 的前
的前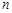 项和
项和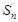 取得最小值,即
取得最小值,即 解得:
解得: ,得
,得 ,故选C.
,故选C.
考点:求数列 的前
的前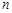 项和
项和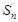 的最值
的最值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设等差数列 的公差
的公差 ,
, ,若
,若 是
是 与
与 的等比中项,则
的等比中项,则 =( )
=( )
| A.3或6 | B.3 | C.3或9 | D.6 |
在 ,三个内角
,三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、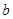 、
、 ,若内角
,若内角 、
、 、
、 依次成等差数列,且不等式
依次成等差数列,且不等式 的解集为
的解集为 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则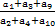 =( )
=( )
A.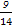 | B.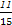 | C. | D.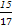 |
已知在等比数列{an}中,有a3a11=4a7,数列{bn}是等差数列,且a7=b7,则b5+b9=( )
| A.2 | B.4 | C.8 | D.16 |
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( ).
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |
在等差数列{an}中,给出以下结论:
①恒有:a2+a8≠a10;
②数列{an}的前n项和公式不可能是Sn=n;
③若m,n,l,k∈N*,则“m+n=l+k”是“am+an=al+ak”成立的充要条件;
④若a1=12,S6=S11,则必有a9=0,其中正确的是( ).
| A.①②③ | B.②③ | C.②④ | D.④ |
已知等差数列{an}满足2a2-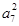 +2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )
+2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )
| A.2 | B.4 | C.8 | D.16 |

