题目内容
若平面向量
,
满足|
|≤1,|
|≤1,且以向量
,
为邻边的平行四边形的面积为
,则
与
的夹角θ的取值范围是 .
| α |
| β |
| α |
| β |
| α |
| β |
| 1 |
| 2 |
| α |
| β |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用平行四边形的面积计算公式、正弦函数的单调性即可得出.
解答:
解:∵以向量
,
为邻边的平行四边形的面积为
,∴|
| |
|sinθ=
.
∵平面向量
,
满足|
|≤1,|
|≤1,
∴
≤sinθ,
∵θ∈(0,π),
∴θ∈[
,
].
∴
与
的夹角θ的取值范围是[
,
].
故答案为:[
,
].
| α |
| β |
| 1 |
| 2 |
| α |
| β |
| 1 |
| 2 |
∵平面向量
| α |
| β |
| α |
| β |
∴
| 1 |
| 2 |
∵θ∈(0,π),
∴θ∈[
| π |
| 6 |
| 5π |
| 6 |
∴
| α |
| β |
| π |
| 6 |
| 5π |
| 6 |
故答案为:[
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查了平行四边形的面积计算公式、正弦函数的单调性,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
设a,b,c∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lga>lgb | ||||
| D、2-a<2-b |
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相交,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,3) | ||||
B、(
| ||||
C、(1,
| ||||
| D、(3,+∞) |
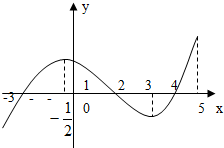 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断: