题目内容
已知一组数据:125 121 123 125 127 129 125 128 130 129 126 124 125 127 126 122 124 125 126 128
(1)填写下面的频率分布表:
| 分组 | 频数 | 频率 |
| [120.5,122.5) | ||
| [122.5,124.5) | ||
| [124.5,126.5) | ||
| [126.5,128.5) | ||
| [128.5,130.5] | ||
| 合计 |
(2)作出频率分布直方图;
(3)根据频率分布直方图或频率分布表求这组数据的众数、中位数和平均数.
[解](1)
| 分组 | 频数 | 频率 |
| [120.5,122.5) | 2 | 0.1 |
| [122.5,124.5) | 3 | 0.15 |
| [124.5,126.5) | 8 | 0.4 |
| [126.5,128.5) | 4 | 0.2 |
| [128.5,130.5] | 3 | 0.15 |
| 合计 | 20 | 1 |
(2)

(3)在[124.5,126.5)中的数据最多,取这个区间的中点值作为众数的近似值,得众数为125.5,(事实上,众数的精确值为125.)
又∵前两个小矩形的频率和为0.25.
∴设第三个小矩形底边的一部分长为x.
则x×0.2=0.25,得x=1.25.
∴中位数为124.5+1.25=125.75.(事实上,中位数为125.5.)
使用“组中值”求平均数:
(事实上,平均数的精确值为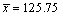 .)
.)

练习册系列答案
相关题目
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
由资料可知y和x呈线性相关关系,由表中数据算出线性回归方程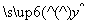 =
= x+
x+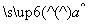 中的
中的 =1.23,据此估计,使用年限为10年时该设备的维修费用约为( )
=1.23,据此估计,使用年限为10年时该设备的维修费用约为( )
A.11.47万元 B.12.38万元
C.12.50万元 D.23.22万元.
 =a,
=a, =b,
=b, =c,则
=c,则 =________.
=________.
 =-4a-1,则实数a的取值范围是________.
=-4a-1,则实数a的取值范围是________. )2a+1<(
)2a+1<(