题目内容
由经验得知,在人民商场付款处排队等候付款的人数及其概率如下:
| 队人数 | 0 | 1 | 2 | 3 | 4 | 5人及以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(2)至少2人排队的概率.
解(1)记没有人排队为事件A,1人排队为事件B.
2人排队为事件C,A、B、C彼此互斥.
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56
(2)记至少2人排队为事件D,少于2人排队为事件A+B,那么事件D与A+B是对立事件,则
P(D)=P( )=1-(P(A)+P(B))=1-(0.1+0.16)=0.74.
)=1-(P(A)+P(B))=1-(0.1+0.16)=0.74.
分析:(1)“至多2人排队”是“没有人排队”,“1人排队”,“2人排队”三个事件的和事件,三个事件彼此互斥,利用互斥事件的概率公式求出至多2人排队的概率.
(2)“至少2人排队”与“少于2人排队”是对立事件;“少于2人排队”是“没有人排队”,“1人排队”二个事件的和事件,二个事件彼此互斥,利用互斥事件的概率公式求出“少于2人排队”的概率;再利用对立事件的概率公式求出)“至少2人排队”的概率.
点评:本题考查互斥事件的概率公式、考查对立事件的概率公式.考查计算能力.
2人排队为事件C,A、B、C彼此互斥.
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56
(2)记至少2人排队为事件D,少于2人排队为事件A+B,那么事件D与A+B是对立事件,则
P(D)=P(
 )=1-(P(A)+P(B))=1-(0.1+0.16)=0.74.
)=1-(P(A)+P(B))=1-(0.1+0.16)=0.74.分析:(1)“至多2人排队”是“没有人排队”,“1人排队”,“2人排队”三个事件的和事件,三个事件彼此互斥,利用互斥事件的概率公式求出至多2人排队的概率.
(2)“至少2人排队”与“少于2人排队”是对立事件;“少于2人排队”是“没有人排队”,“1人排队”二个事件的和事件,二个事件彼此互斥,利用互斥事件的概率公式求出“少于2人排队”的概率;再利用对立事件的概率公式求出)“至少2人排队”的概率.
点评:本题考查互斥事件的概率公式、考查对立事件的概率公式.考查计算能力.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 ”的否定是:________.
”的否定是:________. ,则z=2x•4y的最大值为
,则z=2x•4y的最大值为
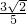 ,若t=
,若t=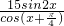 ,则f(t)=________.
,则f(t)=________. 的值.
的值. +
+ =
=