题目内容
如图,在正三棱锥P—ABC中,三条侧棱两两互相垂直,G是△PAB重心,E、F分别在BC、PB上,且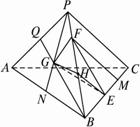
求证:(1)平面GEF⊥平面PBC;
(2)GE是PG与BC的公垂线段.
证明:(1)连结BG,延长交PA于点Q.?
由![]() ,可证明GF∥PA,而PA⊥平面PBC,∴GF⊥平面PBC,GF
,可证明GF∥PA,而PA⊥平面PBC,∴GF⊥平面PBC,GF ![]() 平面EFG.∴平面GEF⊥平面PBC.?
平面EFG.∴平面GEF⊥平面PBC.?
(2)作FM∥PC交BC于M,?
∴![]() ,可得BE=EM=MC.?
,可得BE=EM=MC.?
又FM=FB=![]() PC,?
PC,?
∴在等腰△FBM中,?
可证FE⊥BM,由三垂线定理可证BC⊥GE.?
在△PCB中,作EH⊥PB于H,由平面PBC⊥平面PAB,?
可证EH⊥平面PAB,∴EH∥PC.?
∴![]() .?
.?
设PG∩AB=N,则![]() .?
.?
∴![]() ,HG∥BN.?
,HG∥BN.?
又PN⊥BN,∴HG⊥PN.?
由三垂线定理可证PG⊥GE.?
∴GE与PG、BC垂直且相交,则GE是PG和BC的公垂线段.

练习册系列答案
相关题目
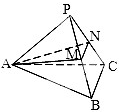 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
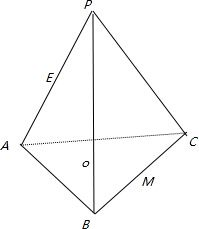 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP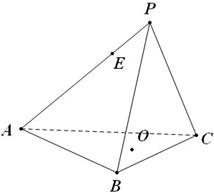 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是. 如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )
如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )