题目内容
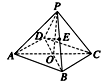
如图所示,在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,
对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.
(1)四棱锥P—ABCD的体积VP—ABCD=![]() ×2
×2![]() ×
×![]() =2.
=2.
(2)异面直线DE与PA所成角的余弦值为![]()
解析:
(1)在四棱锥P—ABCD中,
∵PO⊥平面ABCD,
∴∠PBO是PB与平面ABCD所成的角,
即∠PBO=60°, 2分
在Rt△POB中,
∵BO=AB·sin30°=1,
又PO⊥OB,∴PO=BO·tan60°=![]() ,
,
∵底面菱形的面积S=2×![]() ×2×2×
×2×2×![]() =2
=2![]() .
.
∴四棱锥P—ABCD的体积
VP—ABCD=![]() ×2
×2![]() ×
×![]() =2. 8分
=2. 8分
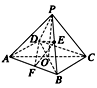
(2)取AB的中点F,连接EF,DF,
∵E为PB中点,∴EF∥PA,
∴∠DEF为异面直线DE与PA所成角(或其补角). 10分
 在Rt△AOB中,
在Rt△AOB中,
AO=AB·cos30°=![]() =OP,
=OP,
∴在Rt△POA中,PA=6,∴EF=![]() . 12分
. 12分
在正三角形ABD和正三角形PDB中,DF=DE=![]() ,
,
由余弦定理得
∴cos∠DEF=![]() 14分
14分
=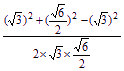 =
=![]() =
=![]() .
.
所以异面直线DE与PA所成角的余弦值为![]() . 16分
. 16分

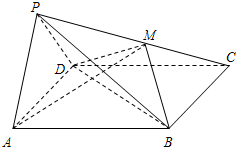 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.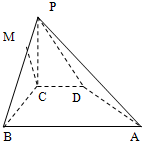 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB