题目内容
(1)求过点(-2,3)的抛物线的标准方程;(2)已知双曲线的离心率等于2,且与椭圆
| x2 |
| 25 |
| y2 |
| 9 |
分析:(1)设出抛物线的方程y2=mx,将过的点代入方程,求出m的值,即得到抛物线的方程.
(2)求出椭圆
+
=1的焦点坐标,设出双曲线的方程,据题意得到参数c的值,根据双曲线的离心率等于2,得到参数a的值,得到双曲线的方程.
(2)求出椭圆
| x2 |
| 25 |
| y2 |
| 9 |
解答:解:(1)若抛物线的焦点在x轴上,设方程为y2=mx,…(1分)
∵抛物线过点(-2,3),
∴32=-2m,
∴m=-
,…(2分)
此时抛物线的标准方程为y2=-
x; …(3分)
若抛物线的焦点在y轴上,设方程为x2=ny,…(4分)
∵抛物线过点(-2,3),∴(-2)2=3n,∴n=
,…(5分)
此时抛物线的标准方程为x2=
y. …(6分)
(2)∵椭圆
+
=1的焦点坐标为(-4,0)和(4,0),…(1分)
设双曲线方程为
+
=1(a>0,b>0),
则c=4,…(2分)
∵双曲线的离心率等于2,即
=2,∴a=2. …(4分)
∴b2=c2-a2=12. …(5分);
故所求双曲线方程为
-
=1. …(6分)
∵抛物线过点(-2,3),
∴32=-2m,
∴m=-
| 9 |
| 2 |
此时抛物线的标准方程为y2=-
| 9 |
| 2 |
若抛物线的焦点在y轴上,设方程为x2=ny,…(4分)
∵抛物线过点(-2,3),∴(-2)2=3n,∴n=
| 4 |
| 3 |
此时抛物线的标准方程为x2=
| 4 |
| 3 |
(2)∵椭圆
| x2 |
| 25 |
| y2 |
| 9 |
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
则c=4,…(2分)
∵双曲线的离心率等于2,即
| c |
| a |
∴b2=c2-a2=12. …(5分);
故所求双曲线方程为
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题主要考查双曲线的简单性质和抛物线的标准方程.解答的关键在于考生对圆锥曲线的基础知识的把握.

练习册系列答案
相关题目
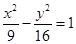 共渐近线,且过点
共渐近线,且过点 ,
求此双曲线C的方程;
,
求此双曲线C的方程;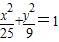 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.