题目内容
已知A、B、C的坐标分别是A(3,0),B(0,3),C(cosα,sinα ).(Ⅰ)若
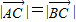 ,求角α 的值;
,求角α 的值;(Ⅱ)若
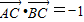 ,求
,求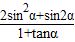 的值.
的值.
【答案】分析:(Ⅰ)先根据A、B、C的坐标分别是A(3,0),B(0,3),C(cosα,sinα ),求出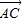 ,
,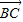 的坐标,再利用
的坐标,再利用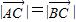 ,就可求出角α 的三角函数值,再根据角α 的三角函数值,求角α 的值.
,就可求出角α 的三角函数值,再根据角α 的三角函数值,求角α 的值.
(Ⅱ)根据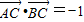 以及前面所求
以及前面所求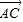 ,
,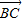 的坐标,就可化简
的坐标,就可化简 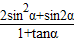 ,进而求值.
,进而求值.
解答:解:(Ⅰ)∵A、B、C的坐标分别是A(3,0),B(0,3),C(cosα,sinα ).
∴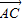 =(cosα-3,sinα),
=(cosα-3,sinα),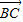 =(cosα,sinα-3)
=(cosα,sinα-3)
∴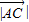 =
=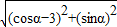 ,
,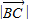 =
=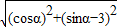
∵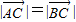 ,∴
,∴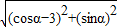 =
=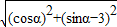
即,(cosα-3)2+(sinα)2=(cosα)2+(sinα-3)2
∴sinα=cosα,∴tanα=1,∴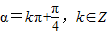
(Ⅱ)由(1)知,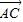 =(cosα-3,sinα),
=(cosα-3,sinα),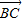 =(cosα,sinα-3)
=(cosα,sinα-3)
∴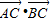 =(cosα-3)cosα+sinα(sinα-3)=1-3(sinα+cosα)=-1
=(cosα-3)cosα+sinα(sinα-3)=1-3(sinα+cosα)=-1
∴sinα+cosα= ,∴(sinα+cosα)2=1+2sinαcosα=
,∴(sinα+cosα)2=1+2sinαcosα=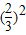
∴2sinαcosα=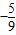
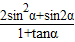 =
=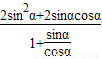 =2sinαcosα=
=2sinαcosα=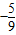
点评:本题考查了向量的模,以及数量积的计算,做题时要细心,避免出错.
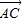 ,
,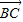 的坐标,再利用
的坐标,再利用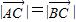 ,就可求出角α 的三角函数值,再根据角α 的三角函数值,求角α 的值.
,就可求出角α 的三角函数值,再根据角α 的三角函数值,求角α 的值.(Ⅱ)根据
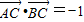 以及前面所求
以及前面所求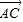 ,
,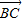 的坐标,就可化简
的坐标,就可化简 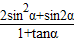 ,进而求值.
,进而求值.解答:解:(Ⅰ)∵A、B、C的坐标分别是A(3,0),B(0,3),C(cosα,sinα ).
∴
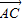 =(cosα-3,sinα),
=(cosα-3,sinα),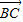 =(cosα,sinα-3)
=(cosα,sinα-3)∴
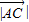 =
=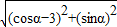 ,
,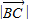 =
=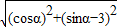
∵
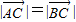 ,∴
,∴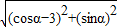 =
=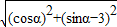
即,(cosα-3)2+(sinα)2=(cosα)2+(sinα-3)2
∴sinα=cosα,∴tanα=1,∴
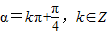
(Ⅱ)由(1)知,
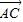 =(cosα-3,sinα),
=(cosα-3,sinα),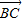 =(cosα,sinα-3)
=(cosα,sinα-3)∴
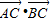 =(cosα-3)cosα+sinα(sinα-3)=1-3(sinα+cosα)=-1
=(cosα-3)cosα+sinα(sinα-3)=1-3(sinα+cosα)=-1∴sinα+cosα=
 ,∴(sinα+cosα)2=1+2sinαcosα=
,∴(sinα+cosα)2=1+2sinαcosα=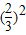
∴2sinαcosα=
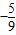
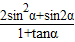 =
=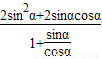 =2sinαcosα=
=2sinαcosα=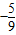
点评:本题考查了向量的模,以及数量积的计算,做题时要细心,避免出错.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目