题目内容
【题目】已知函数![]() ,
,![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若对任意![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 单调递减区间是
单调递减区间是![]() ;当
;当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() .
.
【解析】
试题分析: (1)首先求出函数的导数,然后根据导数的正负解出不等式得到函数的单调区间;(2)求出函数![]() 的导数
的导数![]() ,由
,由![]() 的正负判断函数的单调性并求出函数在
的正负判断函数的单调性并求出函数在![]() 上的值域,当
上的值域,当![]() 时, 不合题意; 当
时, 不合题意; 当![]() 时,判断极值点
时,判断极值点![]() 与端点e的关系,分为
与端点e的关系,分为![]() 时,不合题意;
时,不合题意;![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 上恒成立, 欲使对任意的
上恒成立, 欲使对任意的![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使
,使![]() 成立,则需满足
成立,则需满足![]() ,即
,即![]() .
.
试题解析:(1)![]() ,
,![]() .
.
1)当![]() ,
,![]() ;
;
2)当![]() ,令
,令![]() ,
,![]() ;
;
综上:当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ;
;
当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内递增,在
内递增,在![]() 内递减.又∵
内递减.又∵![]() ,
,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 内的值域为
内的值域为![]() .
.
由![]() ,得
,得![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,不合题意;
上单调递减,不合题意;
②当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .
.
i)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,不合题意;
上单调递减,不合题意;
ii)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
令![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
∴![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() .
.
∴当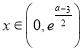 时,
时,![]()
![]() ,
,
且![]() 在
在![]() 上连续.
上连续.
欲使对任意的![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,
,
使![]() 成立,则需满足
成立,则需满足![]() ,即
,即![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() .综上所述,
.综上所述,![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目