题目内容
“a=3”是“直线ax+3y=0和2x+2y=3平行的”
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
C
分析：先判断当a=3成立是否能推出两条直线平行；再判断当两条直线平行时，是否有a=3成立，利用充要条件的定义得到结论．
解答：当a=3时，两条直线的方程分别是3x+3y=0和2x+2y=3，此时两条直线平行成立
反之，当两条直线平行时，有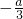
=-1即a=3，
所以“a=3”是“直线ax+3y=0和2x+2y=3平行的”的充分必要条件．
故选C．
点评：判断一个命题是另一个命题的什么条件，也不应该先化简各个命题，再判断是否相互推出．
分析：先判断当a=3成立是否能推出两条直线平行；再判断当两条直线平行时，是否有a=3成立，利用充要条件的定义得到结论．
解答：当a=3时，两条直线的方程分别是3x+3y=0和2x+2y=3，此时两条直线平行成立
反之，当两条直线平行时，有
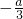=-1即a=3，所以“a=3”是“直线ax+3y=0和2x+2y=3平行的”的充分必要条件．
故选C．
点评：判断一个命题是另一个命题的什么条件，也不应该先化简各个命题，再判断是否相互推出．
练习册系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
a=3是直线ax+2y+3a=0与直线3x+（a-1）y=a-7平行的（ ）
| A、充分非必要条件 | B、必要非充分条件 | C、充要条件 | D、非充分非必要条件 |