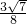Question

一个三角形同时满足：①三边是连续的三个自然数；②最大角是最小角的2倍，则这个三角形最小角的余弦值为（　　）

A． 3 7 8

B． 3 4

C． 7 4

D． 1 8

Answer 1

设三角形三边是连续的三个自然n-1，n，n+1，三个角分别为α，π-3α，2α，
由正弦定理可得：

n-1

sinα

= 

n+1

sin2α

=

n+1

2sinαcosα

，
∴cosα=

n+1

2(n-1)

，
再由余弦定理可得：（n-1）²=（n+1）²+n²-2（n+1）n•cosα=（n+1）²+n²-2（n+1）n•

n+1

2(n-1)

，
化简可得：n²-5n=0，解得：n=5或n=0（舍去），
∴n=5，
则cosα=

n+1

2(n-1)

=

6

8

=

3

4

．
故选B