题目内容
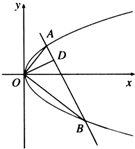 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.分析:A、B两点在抛物线y2=2px上,可设点A(
,y1),B(
,y2),根据向量
、
互相垂直,利用数量积列式,化简得y1y2=-4p2.利用经过两点的斜率公式,得直线AB的斜率为k=
,结合点斜式方程得到直线AB的方程为y-y1=
(x-
),令y=0,化简可得x=2p,所以直线AB经过x轴上的定点M(2p,0).然后根据OD⊥AB,得到直线AB的斜率为-2,最后结合D、M的坐标,可得k=
=-2,解之得p=
.
| y12 |
| 2p |
| y22 |
| 2p |
| OA |
| OB |
| 2p |
| y1+y2 |
| 2p |
| y1+y2 |
| y12 |
| 2p |
| 0-1 |
| 2p-2 |
| 5 |
| 4 |
解答:解:因为A、B两点在抛物线y2=2px上,设点A(
,y1),B(
,y2)
∵
⊥
∴
•
=
•
+y1y2=0⇒y1y2(
+1)=0
∵y1y2≠0,∴
+1=0⇒y1y2=-4p2…①
∵直线AB的斜率为k=
=
∴直线AB的方程为y-y1=
(x-
),
令y=0,得-y1=
(x-
)⇒-y12-y1y2=2px-y12
∴-y1y2=2px…②
将①代入②,得4p2=2px⇒x=2p
所以直线AB经过x轴上的定点M(2p,0)
∵OD⊥AB,OD的斜率为k1=
=
∴直线AB的斜率为k=
=-2,
∴结合D、M的坐标,可得k=
=-2,解之得p=
.
| y12 |
| 2p |
| y22 |
| 2p |
∵
| OA |
| OB |
∴
| OA |
| OB |
| y12 |
| 2p |
| y22 |
| 2p |
| y1y2 |
| 4p2 |
∵y1y2≠0,∴
| y1y2 |
| 4p2 |
∵直线AB的斜率为k=
| y1-y2 | ||||
|
| 2p |
| y1+y2 |
∴直线AB的方程为y-y1=
| 2p |
| y1+y2 |
| y12 |
| 2p |
令y=0,得-y1=
| 2p |
| y1+y2 |
| y12 |
| 2p |
∴-y1y2=2px…②
将①代入②,得4p2=2px⇒x=2p
所以直线AB经过x轴上的定点M(2p,0)
∵OD⊥AB,OD的斜率为k1=
| 0-1 |
| 0-2 |
| 1 |
| 2 |
∴直线AB的斜率为k=
| -1 |
| k1 |
∴结合D、M的坐标,可得k=
| 0-1 |
| 2p-2 |
| 5 |
| 4 |
点评:本题给出过原点的直线与抛物线交于A,B两点,且OA⊥OB,并且已知原点在直线AB上的射影坐标,求抛物线的焦参数值.着重考查了抛物线的简单性质、直线与圆锥曲线间的关系等知识点,属于难题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆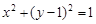 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求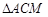 与
与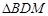 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
