题目内容
函数 ,则y的取值范围是( )
,则y的取值范围是( )A.{y|y≤2}
B.{y|y∈R}
C.{y|0≤y≤2}
D.{y|y≥0}
【答案】分析:由于y′=3+ >0,利用y=3x-
>0,利用y=3x- +1在[-1,0),(0,1]上单调递增的性质可得到答案.
+1在[-1,0),(0,1]上单调递增的性质可得到答案.
解答:解:∵y′=3+ >0,
>0,
∴y=f(x)=3x- +1在[-1,0),(0,1]上单调递增,
+1在[-1,0),(0,1]上单调递增,
∴当x∈[-1,0),ymin=f(-1)=0,当x→0-,y→+∞;
∴当x∈[-1,0),y≥0;①
当x∈(0,1],当x→0+,y→-∞;ymin=f(1)=2;
∴当x∈(0,1],y≤2②
由①②可得:y∈R.
故选B.
点评:本题考查函数的值域,关键在于利用函数的导数的性质研究函数的单调性与最值,难点在于分段研究,取并集,属于中档题.
 >0,利用y=3x-
>0,利用y=3x- +1在[-1,0),(0,1]上单调递增的性质可得到答案.
+1在[-1,0),(0,1]上单调递增的性质可得到答案.解答:解:∵y′=3+
 >0,
>0,∴y=f(x)=3x-
 +1在[-1,0),(0,1]上单调递增,
+1在[-1,0),(0,1]上单调递增,∴当x∈[-1,0),ymin=f(-1)=0,当x→0-,y→+∞;
∴当x∈[-1,0),y≥0;①
当x∈(0,1],当x→0+,y→-∞;ymin=f(1)=2;
∴当x∈(0,1],y≤2②
由①②可得:y∈R.
故选B.
点评:本题考查函数的值域,关键在于利用函数的导数的性质研究函数的单调性与最值,难点在于分段研究,取并集,属于中档题.

练习册系列答案
相关题目
 ,则y的取值范围是( )
,则y的取值范围是( ) B.
B. C.
C. D.
D.
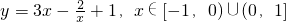 ,则y的取值范围是
,则y的取值范围是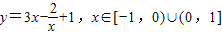 ,则y的取值范围是( )
,则y的取值范围是( ) ,则y的取值范围是
,则y的取值范围是