Question

如图，AB为平面直角坐标系xOy中单位圆O的直径，点D在第二象限内的圆弧上运动，CD与圆O相切，切点为D，且CD=AB．设∠DAB=θ，问当θ取何值时，四边形ABCD的面积最大？并求出这个最大值．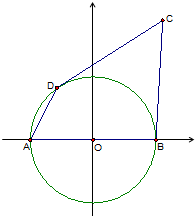

Answer 1

连接BD，
∵AB为平面直角坐标系xOy中单位圆O的直径，点D在第二象限内的圆弧上运动
∴AD=2cosθ，BD=2sinθ（其中

π

4

＜θ＜

π

2

）．…（2分）
在△BCD中，由弦切角定理得∠BDC=θ，又DC=AB=2，
∴△BCD面积为2sin²θ； …（4分）
又Rt△ABD的面积为2sinθ•cosθ．…（5分）
∴四边形ABCD的面积为S=2sinθ•cosθ+2sin²θ．…（6分）
因为S=sin2θ+（1-cos2θ） …（8分）
=

2

sin（2θ-

π

4

）+1 …（10分）
∴2θ-

π

4

=

π

2

，四边形ABCD面积取得最大值
所以当θ=

3π

8

时，四边形ABCD面积取得最大值

2

+1．…（12分）