题目内容
在△ABC中，内角A，B，C所对的边分别是a，b，c，已知a=2，c=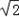
，cosA=-
。
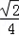（1）求sinC和b的值；
（2）求cos（2A+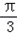
）的值。
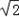，cosA=-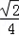。（1）求sinC和b的值；
（2）求cos（2A+
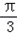）的值。解：（1）△ABC中，由cosA=-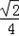
可得sinA=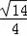
再由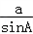
=
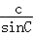以及a=2、c=
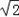，可得sinC=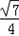
由a2=b2+c2-2bccosA 可得b2+b-2=0，解得b=1。
（2）由cosA=-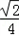
、sinA=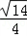
可得 cos2A=2cos2A-1=-
，sin2A=2sinAcosA=-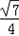
故cos（2A+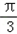
）=cos2Acos
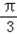-sin2Asin
=
。
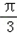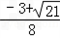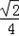可得sinA=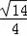再由
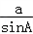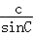= 以及a=2、c=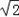，可得sinC=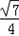由a2=b2+c2-2bccosA 可得b2+b-2=0，解得b=1。
（2）由cosA=-
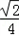、sinA=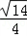 可得 cos2A=2cos2A-1=-
，sin2A=2sinAcosA=-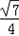故cos（2A+
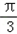）=cos2Acos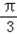-sin2Asin=。
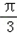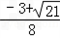练习册系列答案
相关题目